Ciclos Termodinâmicos e Máquinas Térmicas
Um mol de gás ideal monoatômico realiza o ciclo mostrado no diagrama abaixo. No ponto o estado do gás é descrito por , e .
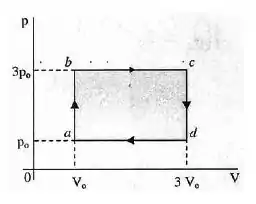
- Em que etapas do ciclo o gás recebe calor da vizinhança, e qual é o calor total recebido?
- Em que etapas do ciclo o gás cede calor para a vizinhança, e qual é o calor total cedido?
- Qual é o rendimento de um motor operando neste ciclo?
- Qual é a variação da entropia do gás no processo ?
Adote: e .
Passo 1
a):
A gente pode deduzir onde ocorre o recebimento de calor pelo gás apenas observando o gráfico. Onde seria? Bom, como em ocorre um crescimento da pressão do gás, assim como em ocorre uma expansão volumétrica do mesmo, podemos concluir que nesses pontos o gás recebeu energia. Logo, foi ali que o gás recebeu calor.
Como calcular esse calor? Pra isso a gente precisa saber a temperatura desses pontos, porque vamos usar:
Como o gás é monoatômico: e . Vamos descobrir as temperaturas de e
Logo, o calor recebido nesse processo foi:
Agora, de pra :
Logo:
Logo, o calor total recebido é :
Passo 2
b):
Aqui a gente pode usar os resultados do item anterior e a relação:
Vamos calcular o trabalho realizado total:
A máquina realiza trabalho nos trechos e , pois é lá que ocorrem variações de volume. Logo:
Usando a relação:
Temos que (lembrando que :
Logo:
A gente usou módulos ali. Você pode representar isso como:
Passo 3
c):
o rendimento é definido por:
Nós já calculamos o trabalho total e o calor recebido, logo:
Passo 4
d):
A variação da entropia é dada por:
Como no processo o fornecimento de calor se dá a pressão constante:
Logo:
Resposta
a):
b):
c):
d):