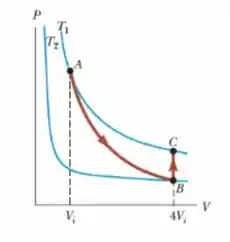
Suponha que mols de gás ideal da figura abaixo se expanda até quatro vezes seu volume inicial. Como se vê, as temperaturas iniciais e finais são as mesmas. Calcule a variação de entropia do gás.
Passo 1
Vamos usar a segunda lei da termodinâmica para responder essa questão. Nela sabemos que:
Logo, podemos afirmar que:
Passo 2
Para um gás ideal equação de Clapeyron descreve perfeitamente o comportamento de um gás, e esta equação é descrita como:
Substituindo a expressão acima, na expressão do passo anterior, chegamos a:
Integrando nossa expressão:
Passo 3
No enunciado temos duas informações muito importantes. A primeira delas é que e que .
Logo, chegamos a nossa resposta final:
Resposta
Letra c
Exercícios de Livros Relacionados
Suponha que 1 m o l de um gás monoatômico ideal inicialmente à pressão p 1 e ocupando um volume V 1 seja submetido sucessivamente a dois processos: ( 1 ) uma expansão isotérmica até um volume 2 V 1 e
Suponha que 0,55 m o l de um gás ideal seja expandido isotérmica e reversivelmente nas quatro situações da tabela abaixo. Qual é a variação da entropia do gás para cada situação?
Quanta energia deve ser transferida na forma de calor para uma expansão isotérmica reversível de um gás ideal a 132 ° C se a entropia do gás aumenta de 46,0J / K ?
Suponha que 4,00m o l s de um gás ideal sofrem uma expansão reversível isotérmica do volume V 1 para o volume V 2 = 2,00 V 1 a uma temperatura T = 400K . Determine (a) o trabalho realizado pelo gás e
Uma caixa de 1,0 L contém N moléculas de um gás ideal, e as posições das moléculas são observadas 100 vezes por segundo. Calcule o temo médio que deve decorrer antes que se possa observar toas as N mo