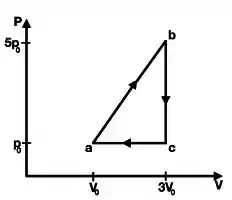
Um mol de gás ideal monoatômico (= 3R/2) realiza um ciclo termodinâmico reversível, como mostrado na figura ao lado. Note que o processo ab é a única etapa em que o gás absorve calor no ciclo, enquanto que sua pressão varia linearmente durante esta expansão. Nos tempos bc e ca o gás libera calor. Determine:
a) O trabalho total realizado pelo gás no ciclo.
b) A eficiência do ciclo.
c) A variação de entropia do gás no processo bc e justifique porque seu resultado não viola a segunda lei da termodinâmica.
Passo 1
a) Entãooooo, o trabalho realizado num processo é a área do gráfico PV abaixo da curva desse processo. Então:
Coloquei esse sinal de menos em porque é uma compressão.
O trabalho no ciclo vai ser:
Passo 2
b) A eficiência do ciclo vai ser:
E olha que maravilha, ele disse que o único processo que o gás recebe calor é o ab. Então:
Vamos calcular .
Usando a 1ᵃ Lei da Termodinâmica:
Já calculamos , então só falta .
Passo 3
Tem uma fórmula pra variação de energia interna:
Em que g é o número de graus de liberdade. Como o gás é manoatômico, g=3.
Só falta a variação de temperatura né? Vamos achar e usando .

E:
Lembrando que n=1!
Voltando lá:
Showwwwww.
Passo 4
Como:
E o rendimento FINALMENTE vai ser:
Passo 5
c) A variação de entropia é:
E o calor no processo vai ser:
Na forma diferencial:
Então:
Só falta né? Vamos calcular:
Substituindo:
Pela 2ᵃ Lei da Termodinâmica, sempre teremos:
Mas tá dando menor que zero né.

É porque a 2ᵃ Lei da Termodinâmica é válida para sistemas! Nosso gás é só uma parte de um sistema maior. No processo teremos um outro subsistema (por exemplo um reservatório) que vai ter uma variação de entropia maior que zero, de modo que:
E aí a variação do sistema inteiro vai ser positiva:
Não contrariando a 2ᵃ Lei da Termodinâmica.
Resposta
a)
b)
c)
Não contraria a 2ᵃ Lei da Termodinâmica porque o gás é só uma parte de um sistema maior.