Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Variação da Entropia de um Gás Ideal

Ver Teoria
Exercício 43123456789101112131415161718192021222324252627282930313233343536373839404142444546474849505152535455565758596061626364

Enunciado

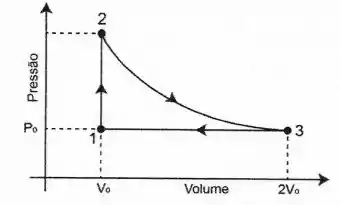
Em uma máquina térmica reversível, um mol de um gás ideal monoatômico sofre uma transformação cíclica representada no diagrama pressão-volume da figura abaixo. O processo termodinâmico 1 → 2 é isocórico, o 2 → 3 é adiabático e o 3 → 1 é isobárico.

  1. Calcule a variação de entropia ∆ S para o ciclo completo.
  2. Calcule as variações de entropia ∆ S 12 , ∆ S 23 e ∆ S 31 para cada um dos processos. Quando possível, expresse seus resultados em termos de R (constante universal dos gases).
  3. Sabendo que a pressão no estado 1 é P 0 , calcule a pressão no estado 2. Expresse seu resultado em termos de P 0 .

Passo 1

  1. Como o processo total é reversível:

    2. ∆ S = 0

    Passo 2

  2. De cara, o processo 2 → 3 é adiabático e reversível, então:

    3. ∆ S 23 = ∫ d Q T = 0

    Passo 3

    O processo 3 → 1 acontece sob pressão constante, logo, podemos dizer que (pela fórmula do “piviti povotó”):

    V 3 V 1 = T 3 T 1

    Substituindo os pontos do gráfico:

    2 V 0 V 0 = T 3 T 1 → T 3 T 1 = 2

    Passo 4

    Como a entropia é calculada por: ∆ S = ∫ d Q T

    Em um processo isobárico nós temos: Q = n C p ∆ T

    Pelo problema, n = 1 , e, assim:

    ∆ S 31 = ∫ T 3 T 1 C p d T T

    ∆ S 31 = C p ln ⁡ T 1 T 3 = C p ln ⁡ 1 2

    Como:   C p = C v + R :

    ∆ S 31 = - C v + R ln ⁡ 2

    Temos que:   C v = g 2 R . No enunciado diz que é um gás monoatômico ( g = 3 ). Vamos ficar, então:

    ∆ S 31 = - 5 R 2 ln ⁡ 2

    Passo 5

    Porém, pela letra (a), vimos que: ∆ S = 0 .

    Logo:

    ∆ S = ∆ S 12 + ∆ S 23 + ∆ S 31 = 0

    Substituindo os valores das entropias encontrados, vamos ter:

    ∆ S 12 = 5 R 2 ln ⁡ 2

    Passo 6

  3. O processo 1 → 2 é isocórico, então, pela fórmula do “piviti povotó”: T 2 T 1 = P 2 P 1

A volume constante:

∆ S 12 = C v ln ⁡ T 2 T 1 = 3 R 2 ln ⁡ P 2 P 1 = 3 R 2 ln ⁡ P 2 P 0

Porém, da letra (b), vimos que: ∆ S 12 = 5 R 2 ln ⁡ 2

Portanto, temos que:

3 R 2 ln ⁡ P 2 P 0 = 5 R 2 ln ⁡ 2

ln ⁡ P 2 P 0 = ln ⁡ 2 5 3

E, finalmente:

P 2 = 2 5 3   P 0

Resposta

  1. ∆ S = 0
  2. ∆ S 12 = 5 R 2 ln ⁡ 2

    3. ∆ S 23 = 0

    ∆ S 31 = - 5 R 2 ln ⁡ 2

  3. P 2 = 2 5 3   P 0

Exercícios de Livros Relacionados

Suponha que 1 m o l de um gás monoatômico ideal inicialmente à pressão p 1 e ocupando um volume V 1 seja submetido sucessivamente a dois processos: ( 1 ) uma expansão isotérmica até um volume 2 V 1 e
Suponha que 0,55 m o l de um gás ideal seja expandido isotérmica e reversivelmente nas quatro situações da tabela abaixo. Qual é a variação da entropia do gás para cada situação?
Quanta energia deve ser transferida na forma de calor para uma expansão isotérmica reversível de um gás ideal a 132 ° C se a entropia do gás aumenta de 46,0J / K ?
Suponha que 4,00m o l s de um gás ideal sofrem uma expansão reversível isotérmica do volume V 1 para o volume V 2 = 2,00 V 1 a uma temperatura T = 400K . Determine (a) o trabalho realizado pelo gás e
Uma caixa de 1,0 L contém N moléculas de um gás ideal, e as posições das moléculas são observadas 100 vezes por segundo. Calcule o temo médio que deve decorrer antes que se possa observar toas as N mo