Primeira Lei e Gases Ideais, Segunda Lei da Termodinâmica, Ciclos Termodinâmicos e Máquinas Térmicas
Um mol de gás ideal monoatômico, partindo sempre do estado inicial de volume , pressão e temperatura , dobra a temperatura por quatro processos diferentes. O processo é a volume constante, o processo é isobárico, o é linear com pressão final e é adiabático. Dê as respostas em função de , e .
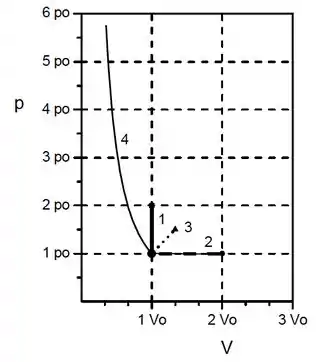
Coloque na tabela os valores da pressão e do volume no final de cada processo. Represente cada processo no diagrama .
Calcule a variação da energia interna para cada um dos processos.
No processo , calcule o trabalho e o calor trocado.
Calcule o trabalho realizado e a variação de entropia nos processos e .
Passo 1
Antes de atacar esse problema, vamos reunir as informações dadas:
Vamos primeiro analisar o processo :
Já sabemos que , vamos então descobrir , para isso, vamos usar a lei dos gases ideais, ao final do processo , temos:
Antes do processo ocorrer, temos:
dividindo a equação dado para o fim do processo pela equação antes do processo começar, temos:
Passo 2
Vamos agora para o processo , utilizaremos o mesmo processo, sabendo que a pressão permanece constante, precisamos apenas determinar o volume:
Ao fim do processo, temos:
Antes de o processo ocorrer, temos:
Dividindo as equeçoes, temos:
Passo 3
Para o processo , já sabemos o valor da pressão final, precisamos determinar o volume, vamos novamente utilizar o mesmo procedimento de antes:
Ao fim do processo, temos:
Antes de o processo ocorrer, temos:
Dividindo as equações, temos:
Passo 4
Agora vamos para o processo . Como se trata de um processo adiabático, teremos:
Para um gás ideal, temos que :
Voltando à equação para o processo, temos:
Agora só falta determinar a pressão, para isso, vamos fazer:
Agora é só montar a tabela e o diagrama:
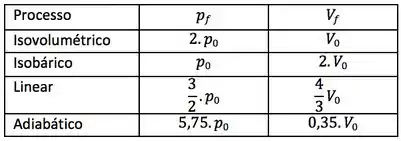
Para o diagrama, teremos:
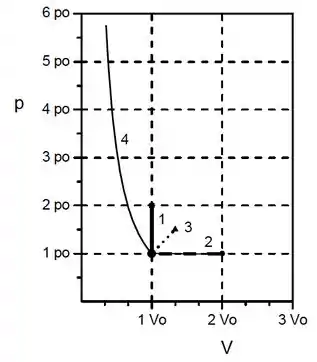
Passo 5
Para determinar a variação da energia interna, vamos relembra a sua definição para gases monoatômicos:
Como a variação de temperatura é a mesma em todos os processos, a variação da energia interna será a mesma em todos os processos:
Sabendo que:
Substituindo na equação da energia interna, temos:
Passo 6
Vamos analisar o processo . Mas primeiramente vamos reunir os dados pertinentes a esse processo:
Para determinar o trabalho, podemos calcular a área abaixo da curva do processo linear, podemos ver, pelo diagrama que se trata de um trapézio, portanto, temos:
Passo 7
Agora que temos o trabalho e a energia intera já calculados, podemos, pela primeira lei da termidinâmica calcular o calor trocado:
Passo 8
Vamos primeiro analisar o processo . Por ser um processo isobárico, temos, que o trabalho é dado por:
Para a variação de entropia, temos:
Substituindo por , temos:
Passo 9
Agora vamos analisar o processo . Por se tratar de um processo adiabático, temos que a troca de calor é zero, portanto, a variação da entropia também é zero!
Agora vamos calcular o trabalho realizado. Pela primeira lei da termodinâmica, temos:
Como temos que , fica:
Ainda bem que já calculamos a variação da energia interna:
Resposta
;
; ; ;
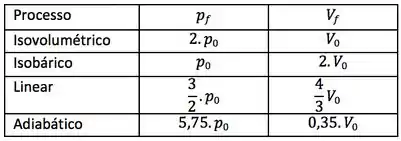