Ciclos Termodinâmicos e Máquinas Térmicas, Segunda Lei da Termodinâmica
Uma máquina térmica operando entre as temperaturas e rejeita
para a fonte fria uma quantidade de calor em um ciclo. Sua eficiência é igual a
da eficiência máxima (Carnot) para essas fontes.
Calcule a quantidade de calor fornecida pela fonte quente e o trabalho realizado em cada ciclo.
Qual deve ser a duraçãoo de cada ciclo para que a potencia média que a máquina entrega seja igual a ?
Essa mesma máquina é utilizada para alimentar um refrigeradore que retira, a cada ciclo (da mesma duraçãoo que o da máquina), uma certa quantidade de calor de um compartimento à temperatura , despejando no ambiente, a uma temperatura , uma quantidade de calor .
Faça um esquema do funcionamento do sistema composto,indicando com setas os fluxos de energia.
Sendo , obtenha o coeficiente de desempenho do refrigerador.
Calcule a variação de entropia do sistema [refrigerador compartimento a ambiente a ] após um ciclo. O resultado é compatível com a segunda lei da termodinâmica?
Passo 1
Como temos a eficiência da máquina, podemos determinar o calor recebido da fonte quente, assim como o trabalho realizado pelo ciclo somente pela equação de rendimento, se liga!
Vamos primeiro determinar a eficiência da máquina:
Sabendo que a eficiência máxima é a de um ciclo de Carnot, temos:
Passo 2
Agora que temos a eficiência, vamos calcular o calor recebido da fonte quente :
substituindo os valores, temos:
Para determinar o trabalho, temos:
Passo 3
Para determinar a duração do ciclo, vamos relembrar a definição de potência:
substituindo os valores que temos, podemos achat o tempo:
Se liga que o trabalho está em e a potência está em , por isso não multiplicamos por , pois iria cancelar de qualquer maneira!
Passo 4
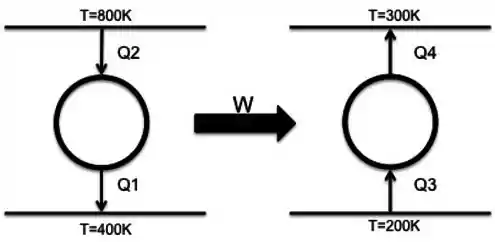
Para os ciclos descritos, teremos o seguinte esquema:
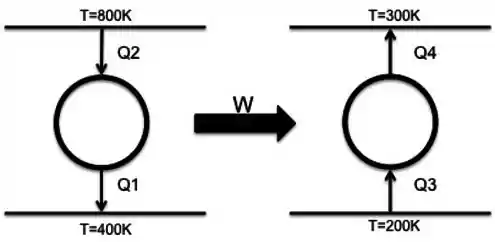
Passo 5
Para um refrigerador, temos a seguinte definição de desempenho:
Para o nosso sistema, fica:
No entanto, precisamos determinar , para isso, fazemos:
Substituindo na equação do desempenho, temos:
Passo 6
Para calcular a entropia do sistema, vamos primeiro calcular a entropia de cada componente separadamente:
Vamos começar com a do refrigerador:
Como o refrigerador retorna ao seu estado inicial, a entropia é nula!
Passo 7
Para o compartimento a , temos:
Lembrando que como o calor é retirando do compartimento, teremos que a entropia é negativa!
Como sabemos que , fica:
Calma...a conta está correta...como tínhamos em , simplesmente multiplicamos o resultado final por !
Passo 8
Para o ambiente a , temos:
Lembrando novamente que passamos de para !
Passo 9
Para o sistema como um todo, temos:
Tal resultado não é compatível com a segunda lei da termodinâmica, pois a entropia total não pode ser negativa, ou sej anão pode diminuir.
Resposta
;
Não é compatível com a segunda lei da termodinâmica, pois .