Um mol de gás diatômico ideal tem seu estado inicialicaracterizado por uma pressão e um volume . O gás é aquecido através de dois processos termodinâmicos. O primeiro processo é a volume constante e o segundo a pressão constante. O estado termodinâmico final f do gás é caracterizado por uma pressão 3 vezes maior do que a inicial e um volume 2 vezes maior do que o inicial. Considere que as temperaturas envolvidas nos processos não ativam graus de liberdade vibracionais do gás. Dê suas respostas em termos de, e R, a constante dos gases ideais.
a) Desenhe o diagrama P-V indicando claramente o estado final e o inicial do gás e sua trajetória de processos termodinâmicos.
b) Calcule a quantidade de calor absorvida ou retirada pelo gás ao ir de seu estado inicial i ao final f.
c) Calcule a variação da entropia do gás ao ir do estado inicial i ao final f.
Observação: Qualquer resultado que não esteja fornecido no formulário em anexo deve ser DEMONSTRADO.
Passo 1
a) Então, nós vamos ter um estado intermediário entre os pontos i e f que eu vou chamar de A, ok?
Então pensa comigo: do estado i ao estado A temos uma transformação a volume constante. Então vai ser uma reta vertical!
Do estado A ao estado f vamos ter uma transformação a pressão constante. Isso quer dizer que vai ser uma reta horizontal!
Colocando os valores da pressão e do volume em todos os estados, vai ficar mais ou menos assim:
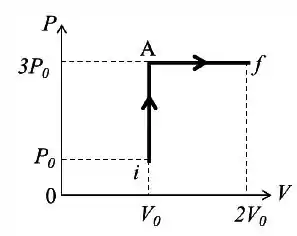
Passo 2
b) Primeiro vamos calcular as temperaturas nos três pontos. Vamos usar:
Como temos um mol de gás, então , o que simplifica as nossas contas :D
Então, no ponto i:
No ponto A:
No ponto f:
Passo 3
Beleza! Agora que temos as temperaturas vamos calcular o calor nos dois processos. Repare que um processo é a volume constante outro a pressão constante.
No processo :
Vamos lembrar que pra um gás diatômico, .
No processo :
E .
Passo 4
Então no processo a gente vai ficar com:
Passo 5
c) Pra variação de entropia a gente tem que usar essa fórmula:
No processo :
No processo :
Passo 6
A variação de entropia total então vai ser:
Resposta
a)
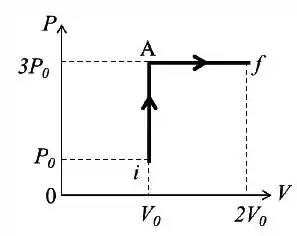
b)
c)