Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Variação da Entropia de um Gás Ideal

Ver Teoria
Exercício 24123456789101112131415161718192021222325262728293031323334353637383940414243444546474849505152535455565758596061626364

Enunciado

Um gás ideal cujo calor específico é c V = 5 / 2   R , realiza o ciclo A B C A representado no diagrama p V na figura.

Considere n R   =   100   J / K ,   p 0 = 1,0 × 10 5   P a   e   V 0 =   0,10   m 3 .

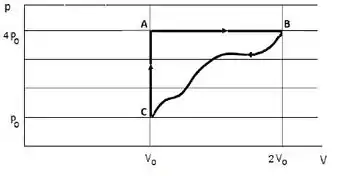
(a) Calcule as temperaturas nos pontos T B   e   T C de funcionamento do ciclo

(b) Se o trabalho realizado pelo gás em cada ciclo é 13 k J , calcule o trabalho no trecho B C , explicitando se é realizado ou recebido pelo gás.

(c) A eficiência deste sistema operando como uma máquina térmica é 0,06. É compatível este resultado com o esperado de acordo com a segunda lei da termodinâmica? (compare a eficiência com a de uma máquina de Carnot funcionando entre as mesmas temperaturas extremas).

(d) Para cada ciclo, determine o calor que deve ser fornecido ao gás e o calor que o sistema perde.

(e) Qual é a variação de entropia do gás no processo BC?

(f) Este gás é monoatômico, diatômico ou poliatômico? Justifique.

Passo 1

(a) Vamos utilizar a equação de Clapeyron para descobrirmos as temperaturas de B e C, já que temos as outras informações em cada ponto.

p V = n R T   → T = p V n R

Então

T B = 4 p o 2 V o n R = 8 × 10 5 × 0,1 100 = 800 K

T C = p o V o n R = 1 00 K

Passo 2

(b) O trabalho do ciclo será a soma do trabalho realizado em cada processo

W c = W A B + W B C + W C A

O processo C A é um processo isocórico, ou seja, não há variação do volume, logo W C A = 0 .

W A B = 4 p o 2 V o - V o = 4 p o V o = 40 k J

W B C = W C - W A B = 13   k J - 40 k J = - 27 k J

Logo o gás recebe 27   k J de trabalho no processo B C .

Passo 3

(c) Vamos calcular a eficiência de Carnot para analisarmos se satisfaz a 2 lei.

ε = T Q - T F T Q = 800 - 100 800 = 0,875

Como a eficiência da máquina térmica (0,06) é menor que a eficiência de Carnot, então satisfaz 2º lei.    

Passo 4

(d) Sabemos pelas informações que

T A = 4 p o V o n R = 400   K

Então vamos calcular a quantidade de calor perdida ou recebida em cada processo:

Q A B = n c p ∆ T = 7 2 n R T B - T A = 7 2 × 100 × 800 - 400 = 140 k J

Q B C = ∆ E B C + W B C = n c V T c - T b + W B C = - 175 - 27 k J = - 202   k J

Q C A = ∆ E C A = n c V T A - T C = 5 2 × 100 × 400 - 100 = 75   k J

Então

Q p e r d i d o = 202   k J

Q f o r n e c i d o = 215   k J

Passo 5

(e)

d Q = d E + p d V = n c V d T + n R T V d V

Logo

∆ S B C = ∫ B C d Q T = n c V ln ⁡ T C T B + n R ln ⁡ V C V B

∆ S = 5 2 n R l n 100 800 + n R l n 1 2 = - 589,2 J K

Passo 6

(f) a capacidade calorifica a volume constante do gás é 5/2. Ou seja, o número de graus de liberdade é 5 (3 de translação e 2 de rotação). Logo, o gás é diatômico.    

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Suponha que 1 m o l de um gás monoatômico ideal inicialmente à pressão p 1 e ocupando um volume V 1 seja submetido sucessivamente a dois processos: ( 1 ) uma expansão isotérmica até um volume 2 V 1 e
Suponha que 0,55 m o l de um gás ideal seja expandido isotérmica e reversivelmente nas quatro situações da tabela abaixo. Qual é a variação da entropia do gás para cada situação?
Quanta energia deve ser transferida na forma de calor para uma expansão isotérmica reversível de um gás ideal a 132 ° C se a entropia do gás aumenta de 46,0J / K ?
Suponha que 4,00m o l s de um gás ideal sofrem uma expansão reversível isotérmica do volume V 1 para o volume V 2 = 2,00 V 1 a uma temperatura T = 400K . Determine (a) o trabalho realizado pelo gás e
Uma caixa de 1,0 L contém N moléculas de um gás ideal, e as posições das moléculas são observadas 100 vezes por segundo. Calcule o temo médio que deve decorrer antes que se possa observar toas as N mo