Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Vetor Velocidade e Vetor Tangente

Ver Teoria
Exercício 34123456789101112131415161718192021222324252627282930313233353637

Enunciado

Considere a curva C definida pela função vetorial

r t = t s e n π t ,   t c o s π t ,   t 2

Onde t ≥ 0 .

a) Mostre que a curva C está contida em uma superfície quádrica. Identifique essa superfície e use esse fato para esboçar a curva C .

b) Encontre a equação simétrica a reta tangente à curva C no ponto P 0 ,   - 1 ,   1 .

Passo 1

a) Isso pode ser muito tranquilo se você conseguir enxergar isso que vou te mostrar agora:

r t = t cos ⁡ π t ,   t   s e n π t ,   t 2 ,   t ≥ 0 .

x = t cos ⁡ π t

y = t   s e n   π t

z = t 2

Observe a relação s e n 2 π t + cos 2 ⁡ π t = 1

Observe ainda que x 2 + y 2 = z → t 2 s e n 2 π t + t 2 cos 2 ⁡ π t = t 2 → t 2 s e n 2 π t + cos 2 ⁡ π t = t 2 → t 2 = t 2

Passo 2

Então sabemos que x 2 + y 2 = z realmente é parametrizado por:

r t = t cos ⁡ π t ,   t   s e n π t ,   t 2 ,   t ≥ 0

Então a curva que procuramos está contida na superfície x 2 + y 2 = z  

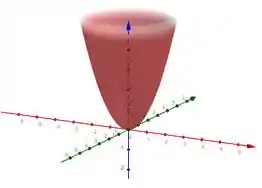
Passo 3

b) vamos começar essa b identificando o instante t em que r t = t s e n π t ,   t c o s π t ,   t 2   passa pelo ponto P 0 ,   - 1 ,   1 .

t s e n π t = 0 t c o s π t = - 1 t 2 = 1

O único t que satisfaz essas 3 condições é t = 1 .

A fórmula da equação simétrica para a reta tangente a curva será representada por:

R s = r 1 + s . r ' 1

Vamos então precisar da derivada da nossa curva.

r t = t s e n π t ,   t c o s π t ,   t 2

r ' t = ( s e n π t + π t c o s π t , cos ⁡ π t - π t s e n π t ,   2 t )

r ' 1 = 0 - π ,   - 1 + 0 ,   2 = ( - π ,   - 1 ,   2 )

Calculando então a equação da reta:

R s = r 1 + s . r ' 1

R s = 0 ,   - 1 ,   1 + s - π ,   - 1 ,   2

Resposta

a )   x 2 + y 2 = z

b )   R s = 0 ,   - 1 ,   1 + s - π ,   - 1 ,   2

Exercícios de Livros Relacionados

(Regra da Cadeia). Sejam t → u t ,t ∈ I , u → F → u ∈ R n ,u ∈ J , funções deriváveis, onde I e J são intervalos em R . Suponha que, para todo t ∈ I , u t ∈ J . Prove que a função H → dada por H → t =
Calcule (d vec F)/(d t) e (d^2 vec F)/(d t^2) .vec F (t) = (3 t^2 , e^(- t) , ln ( t^2 + 1 ))
Suponha que μ p θ =c o s θ i - +s e n θj - , u θ θ =- s e n θi - + c o s θj - , r t = p t u p ( θ ( t ) ) , com θ = θ ( t ) e p = p ( t ) deriváveis até a segunda ordem no intervalo I . N o t a ç ã o
Determinar a derivada das seguintes funções vetoriais:d) f → t = e - t i → + e - 2 t j → + k →
Determinar a derivada das seguintes funções vetoriais:e) g → t = ln ⁡ t i → + tj → + tk →