Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Vetor Velocidade e Vetor Tangente

Ver Teoria
Exercício 29123456789101112131415161718192021222324252627283031323334353637

Enunciado

UFES, Cálculo I, P2, 2020.2, questão 3

Duas pessoas começam a andar a partir do mesmo ponto. Uma vai para o leste a 6   k m / h e a outra, para o sul a 12   k m / h . Quão rápido está variando a distância entre as pessoas após 30   m i n u t o s ?

Passo 1

Faaaala, galeraaaa! Tudo beleza?

O objetivo dessa questão é obter a distância em um dado momento entre dois pontos que neste caso, são duas pessoas caminhando para diferentes direções.

Para resolver essa questão vamos adotar que o leste está no sentido positivo de y e que o sul está no sentido positivo de x . Como mostra a figura abaixo.

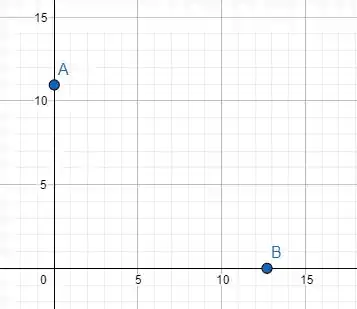
Vamos organizar os dados para conseguir calcular o que se pede no enunciado.

Sabemos que o ponto A é composto por:

x A = 6 t

y A = 0

E que o ponto B é composto por:

x B = 12 cos ⁡ ( 90 ) t = 0

y B = 12 sin ⁡ 90 t = 12 t

A justificativa para o ângulo de 90   ° pode ser vista na figura abaixo. Note que o ângulo formado entre leste e sul é 90   ° .

Passo 2

Agora o que precisamos é somente substituir os dados que obtivemos na fórmula da distância. Assim, temos

d A B = ( x B - x A ) 2 + ( y B - y A ) 2

d A B = ( 0 - 6 t ) 2 + ( 12 t - 0 ) 2

d A B = t 2 ( 0 - 6 ) 2 + t 2 ( 12 - 0 ) 2

d A B = t 2 ( - 6 ) 2 + t 2 ( 12 ) 2

d A B = t 2 ( 36 ) + t 2 ( 144 )

Resolvendo a raíz quadrada de t  

d A B = t ( 36 + 144 )

d A B = t ( 180 )

d A B = 13,41 t

Passo 3

O último passo dessa questão é substituir o tempo de 30 minutos na expressão obtida no Passo 2.

d A B = 13,41 t

30   m i n u t o s = 0,5   h o r a s

Substituindo

d A B = 13,41 0,5 = 6,7   k m / h

Prontinho, até mais!

Resposta

d A B = 6,7   k m / h

Exercícios de Livros Relacionados

(Regra da Cadeia). Sejam t → u t ,t ∈ I , u → F → u ∈ R n ,u ∈ J , funções deriváveis, onde I e J são intervalos em R . Suponha que, para todo t ∈ I , u t ∈ J . Prove que a função H → dada por H → t =
Calcule (d vec F)/(d t) e (d^2 vec F)/(d t^2) .vec F (t) = (3 t^2 , e^(- t) , ln ( t^2 + 1 ))
Suponha que μ p θ =c o s θ i - +s e n θj - , u θ θ =- s e n θi - + c o s θj - , r t = p t u p ( θ ( t ) ) , com θ = θ ( t ) e p = p ( t ) deriváveis até a segunda ordem no intervalo I . N o t a ç ã o
Determinar a derivada das seguintes funções vetoriais:d) f → t = e - t i → + e - 2 t j → + k →
Determinar a derivada das seguintes funções vetoriais:e) g → t = ln ⁡ t i → + tj → + tk →