Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Vetor Velocidade e Vetor Tangente

Ver Teoria
Exercício 18123456789101112131415161719202122232425262728293031323334353637

Enunciado

Integral de Linha – Caso Escalar

Sejam a , b ∈ R tais que 0 < a ≤ b . Considere a curva C representada parametricamente por r : 0,2 π → R 2 , r t = a cos ⁡ t ,   b sen ⁡ t

  1. Desenhe o traço e o gráfico de C . Justifique.

c) Assuma b = 2 a . Determine os vetores velocidade da curva C em cada ponto de interseção da curva com os eixos x e dos y e represente-os graficamente.

Passo 1

a )

O traço vai ser a curva r t no plano x y , vamos entender essa parametrização r t . Repara que se dividirmos x por a e y por b vamos sobra com cosseno e seno, isso nos diz que

x a 2 + y b 2 = cos ⁡ t 2 + sen ⁡ t 2 = 1

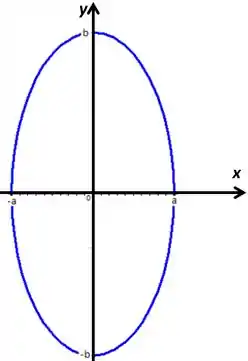
Isso é uma elipse centrada na origem com eixos a em x e b em y , o traço vai ficar

Passo 2

Vamos ver agora essa curva C , primeiro temos que entender como ela é. A curva vai ser

r : 0,2 π → R 2

Isso nos diz que t vai de 0 à 2 π , além disso vamos ter

x = t

E

y , z = r t

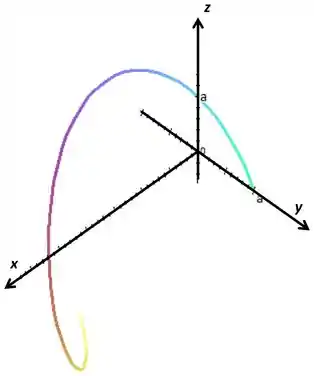
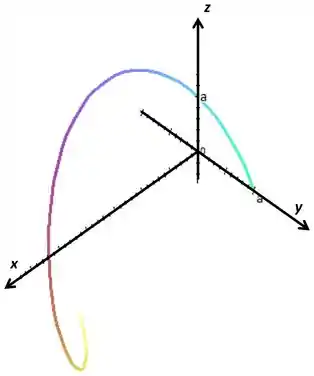
Então a curva C vai ser

C t = t , a cos ⁡ t ,   b sen ⁡ t

Isso vai ser uma hélice elíptica sobre o eixo do x , vamos ver onde começa e onde termina essa parada, ele vai começar com t = 0

C 0 = 0 , a cos ⁡ 0 , b sen ⁡ 0 = 0 , a , 0

Agora com t = 2 π

C 2 π = 2 π , a cos ⁡ 2 π , b sen ⁡ 2 π = 2 π , a , 0

Passo 3

c )

Dessa vez r t vai ficar

r t = a cos ⁡ t ,   2 a sen ⁡ t

Isso porque ele disse que b = 2 a

Ele quer os vetores velocidade da curva em alguns pontos. Vamos primeiro entender como vamos achar esse vetor velocidade, lembra que vamos ter

v C t = r ' t

Isso nos diz que

v C t = - a sen ⁡ t , 2 a cos ⁡ t

Se olharmos o gráfico de r t , da um look aqui em baixo,

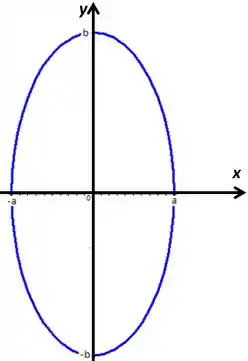
O t é o ângulo que vamos rodando ao longo da elipse, isso nos diz que os pontos que ele quer são 0 , π 2 , π , 3 π 2 . Então vamos achar a velocidade nesse pontos,

Entendo que no eixo y temos t = π 2 e t = 3 π 2 , enquanto que no eixo x temos t = 0 e t = π

Vamos aos pontos:

Eixo x :

v C 0 = - a sen ⁡ 0 , 2 a cos ⁡ 0 = 0 , a ∙ 1 = 0,2 a

v C π = - a sen ⁡ π ,   2 a cos ⁡ π = 0 , a ∙ - 1 = 0 , - 2 a

Eixo y :

v C π 2 = - a sen ⁡ π 2 ,   2 a cos ⁡ π 2 = - a ∙ 1,0 = - a , 0

v C 3 π 2 = - a sen ⁡ 3 π 2 ,   2 a cos ⁡ 3 π 2 = - a ∙ - 1 , 0 = a , 0

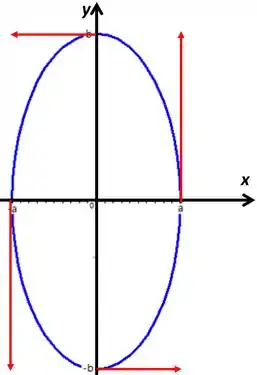
Isso graficamente vai ficar

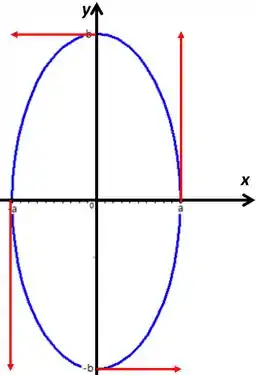
Os valores da velocidade no eixo y vão ter o tamanho do eixo x da elipse, que é a , enquanto os valores da velocidade no eixo x vão ter o tamanho do eixo y da elipse, que é 2 a .

Resposta

c.

Exercícios de Livros Relacionados

(Regra da Cadeia). Sejam t → u t ,t ∈ I , u → F → u ∈ R n ,u ∈ J , funções deriváveis, onde I e J são intervalos em R . Suponha que, para todo t ∈ I , u t ∈ J . Prove que a função H → dada por H → t =
Calcule (d vec F)/(d t) e (d^2 vec F)/(d t^2) .vec F (t) = (3 t^2 , e^(- t) , ln ( t^2 + 1 ))
Suponha que μ p θ =c o s θ i - +s e n θj - , u θ θ =- s e n θi - + c o s θj - , r t = p t u p ( θ ( t ) ) , com θ = θ ( t ) e p = p ( t ) deriváveis até a segunda ordem no intervalo I . N o t a ç ã o
Determinar a derivada das seguintes funções vetoriais:d) f → t = e - t i → + e - 2 t j → + k →
Determinar a derivada das seguintes funções vetoriais:e) g → t = ln ⁡ t i → + tj → + tk →