Calcule a integral , onde e é a curva dada pela interseção do cone com o plano orientada no sentido anti-horário
quando visto de cima.
Passo 1
Oiie, tudo certinho com você?
Queremos calcular a seguinte integral de linha
em que temos um campo vetorial da forma , e uma curva obtida da intersecção do cone
com o plano , esta curva orientada no sentido anti-horário quando vista de cima. Esse último comentário é uma dica que é conveniente para nós utilizar o teorema de Stokes, temos que o teorema diz o seguinte
Vamos tentar escrever a nossa integral em termos do lado esquerdo do teorema acima! E, então, checar se realmente é mais conveniente! Bora lá!
Passo 2
Primeiramente, vamos calcular o rotacional do campo vetorial, temos que
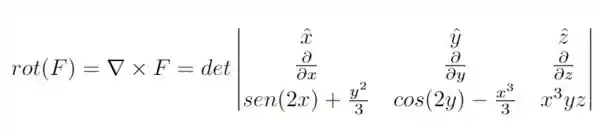
Se calcularmos o determinante, temos que
lembrando que variáveis que não estão sendo derivadas pela derivada parcial são tomadas como constantes, podemos escrever que
Portanto, a nossa integral tem o seguinte formato
Ainda precisamos escrever o elemento de superfície , e para isso, iremos precisar de uma parametrização! Vamos tentar encontrar uma!
Passo 3
Podemos tentar parametrizar utilizando coordenadas polares da forma
Quem é ? Pela equação do cone, temos que
Portanto, usando as parametrizações para e , e o fato que , temos a seguinte
A parametrização é então, a seguinte
Usando esta parametrização, vamos reescrever a nossa integral de superfície como
Precisamos então calcular o produto vetorial e fazer o produto escalar! Tem bastante continha! Mas nada muito complicado! Vamo que vamo!
Passo 4
Primeiro vamos calcular os vetores tangentes, para isso vamos derivar parcialmente a nossa parametrização, temos que
e, também, temos que
Se fizermos o produto vetorial entre os ambos vetores para encontrar o vetor normal a nossa superfície, temos que
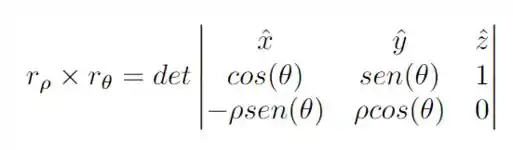
Expandindo o determinante, obtemos que
Ou, simplificando a expressão, e usando novamente que , obtemos
Maravilha! Com isso já estamos perto de termos tudo que precisamos para resolver a nossa integral! Precisamos fazer o produto escalar do campo vetorial nas coordenadas da parametrização com o vetor normal acima! Vem comigo!
Passo 5
Temos que o produto escalar é da forma
Expandindo o produto, temos que
Utilizando este resultado e que o elemento de área em coordenadas polares é , temos que
Uff… Agora faltam apenas os limites de integração! Como temos que o cone intercepta nossa curva em , temos que a intersecção nos dá a seguinte circunferência
Como essa é uma circunferência de raio , então temos que e . A nossa integral pode ser então finalmente, dividida em uma soma de integrais duplas da forma
Algumas integrais aqui são mais simples que outras! Vamos resolver uma de cada vez, belezinha?
Passo 6
A primeira coisa boa de termos escolhido esta parametrização é que as nossas integrações em e podem ser feitas em qualquer ordem, sem afetarem uma à outra. Portanto, podemos usar a seguinte primitiva para identificar as integrais em , temos que
ou, simplesmente, temos que
Usando isso em todas as integrais duplas, podemos reduzir o problema à
De forma que nos resta resolver as seguintes integrais simples
Destas integrais algumas são mais simples que outras, o segredo nas mais complicadas é utilizar as relações de ângulo duplo! Saca só!
Passo 7
Temos primeiro a seguinte integral que é mais direta
como temos que , esta integral resulta em
Agora, vamos resolver a seguinte integral
Para essa vamos utilizar a relação de ângulo duplo, ou seja, usar que
Isso simplifica bastante a nossa integral, uma vez que obtemos
A primeira integral é bastante direta, nós temos que
Para a segunda integral, nós temos que
Pois temos que . Esta integral toma então a forma
Duas já foram! Vamos dar uma pausa e beber uma água! E, resolver as duas que faltam! Bora para o próximo passo!
Passo 8
Temos que resolver ainda a seguinte integração
vamos usar a relação de duplo ângulo tanto para o que já usamos no passo anterior, e para o como
A nossa integral fica então como
A primeira integral novamente é bastante direta, temos que
como fizemos no passo anterior, e temos que usar para a segunda integral, novamente a relação de ângulo duplo, de forma que
A primeira integral já resolvemos algumas vezes, ela resulta em , a segunda é dada por
Pois temos que . Juntando todos os resultados, temos que integral original é
Ainda falta mais uma integral! Calma lá! Que estamos quase acabando! Saca só!
Passo 9
A integral que falta é essa
usando a relação de ângulo duplo, temos que
expandindo o produto iremos obter três integrais que já resolvemos antes, temos que
Juntando os resultados anteriores, temos que
Maravilha! Temos então finalmente que a integral que queríamos desde o começo será
A questão é isso! Te vejo na próxima! Tchau Tchau!