Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campos e Operadores Vetoriais

Ver Teoria
Exercício 1812345678910111213141516171920212223242526272829303132333435363738394041

Enunciado

USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 2 - 2022.1, Questão 25d

Calcule

d) ∫ γ 2 x y + sin ⁡ y d x + x cos ⁡ y d y + x 2 d z onde γ é a intersecção das superfícies 3 x 2 + y 2 + z 2 = 1 e y = x , no 1º octante e orientada de forma que sua projeção no plano y z seja percorrida no sentido horário.

Passo 1

Olá meu amigo, Yuri aqui e irei lhe ajudar a resolver essa atividade. Antes de tudo, vamos dar uma olhada em γ .

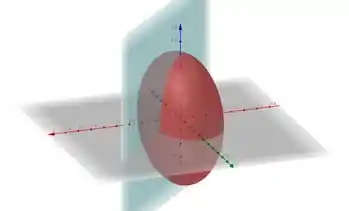
A junção entre 3 x 2 + y 2 + z 2 = 1 e y = x é mostrada na figura acima. A projeção de γ em zy é dada por

3 x 2 + y 2 + z 2 = 1

4 y 2 + z 2 = 1

x ≥ 0

y ≥ 0

z ≥ 0

Vamos agora parametrizar 4 y 2 + z 2 = 1

Que é a nossa γ

y = sin ⁡ t 2

z = cos ⁡ t

γ t = sin ⁡ t 2 , sin ⁡ t 2 , cos ⁡ t ,   t ∈ 0,2 π

Passo 2

Calculando nossa integral de linha utilizando a parametrização que acabamos de fazer

∫ 0 2 π ( 2 sin ⁡ t 2 ∙ sin ⁡ t 2 + sin ⁡ ( sin ⁡ t 2 ) ) ∙ cos ⁡ t 2 d t + sin ⁡ t 2 ∙ cos ⁡ sin ⁡ t 2 ∙ cos ⁡ t 2 d t + sin 2 ⁡ t 4 - sin ⁡ t d t

Continuando com o nosso calculo fazendo os produtos

∫ 0 π 2 sin 2 ⁡ t cos ⁡ t 4 d t   + ∫ 0 π 2 cos ⁡ t 2 ∙ sin ⁡ sin ⁡ t 2 d t + ∫ 0 π 2 sin ⁡ t ∙ cos ⁡ t 4 cos ⁡ - sin ⁡ t 2 d t - ∫ 0 π 2 sin 2 ⁡ t sin ⁡ t 4 d t

Para realizar esses cálculos, iremos utilizar uma substituição

u = sin ⁡ t

d u = cos ⁡ d t

d t = d u cos ⁡ t

Calculando utilizando essa substituição

∫ 0 1 u 2 ∙ cos ⁡ t 4 ∙ d u cos ⁡ t + ∫ 0 1 cos ⁡ t 2 sin ⁡ u 2 ∙ d u cos ⁡ t + ∫ 0 1 u ∙ cos ⁡ t 4 ∙ cos ⁡ u 2 ∙ d u cos ⁡ t - 1 4 - cos ⁡ t sin 2 ⁡ t 3 0 π 2 + 2 3 ∫ 0 π 2 sin ⁡ t d t = 1 12 + ∫ 0 1 1 2 sin ⁡ u 2 d u + u ∙ 2 sin ⁡ u 2 4 - ∫ 0 1 1 2 sin ⁡ u 2 d u - 1 4 ∙ 2 3 - cos ⁡ π 2 - cos ⁡ 0

= 1 12 + 1 2 sin ⁡ 1 2 - 1 6

= 1 12 6 sin ⁡ 1 2 - 1

Resposta

= 1 12 6 sin ⁡ 1 2 - 1

Exercícios de Livros Relacionados

Calcule int_c (x - y + z - 2) d s onde C é o segmento de reta x = t , y = (1 - t) , z = 1 de (0,1 , 1) a ( 1,0 , 1 )
Sejam vec f = (x z , z y , x y) e vec g = (x^2 , y^2 , z^2) .Determinar:g) (grad xx vec f) * (grad xx vec g)
Verificar se as seguintes funções são harmônicas em algum domínio.b) f x , y = 2 x 2 - y 2 + y + 10
Verificar se o campo dado é irrotacional.c) vec f (x , y , z) = (y z e^(x y z) , x z e^(x y z) , x y e^(x y z))
Verificar se as seguintes funções são harmônicas em algum domínio.a) f x , y , z = z x + ln ⁡ x y