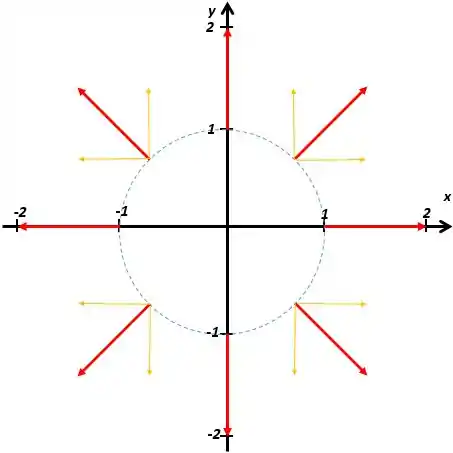
Desenhe o campo radial
Juntamente com suas componentes verticais e horizontais em um conjunto representativo de pontos da circunferência
Passo 1
Então, pessoal, aqui para podermos desenhar o campo radial, vamos antes ter que entender como é o conjunto e definir alguns pontos para representar. Ele também forneceu as componentes horizontais e verticais, e a partir delas conseguimos traçar a resultante e desenhar o campo radial.
Como o exercício pede um conjunto representativo na cicunferência , podemos representar os pontos em que a circunferência corta os eixos e . Esses pontos seriam:
Mas também precisamos entender como é esse campo, quando não estamos em cima do eixo. Neste caso, podemos escolher os pontos “médios”, onde e são iguais em módulo:
Então a figura do conjunto representativo com os pontos selecionados ficou assim:
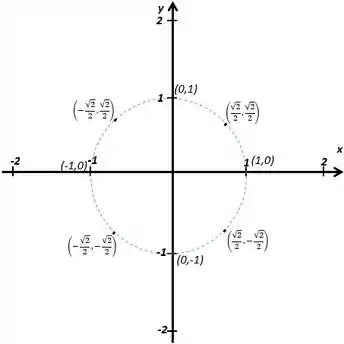
É valido ressaltar aqui, que poderiaos escolher outros pontos para desenhar, mas eles teriam que estar sobre a linha pontilhada azul da circunferência.
Passo 2
O enunciado forneceu esse campo radial:
Ou seja, as componentes horizontais são dadas por , e verticais, dadas por . Nesse caso temos e .
Então para cada um dos pontos vamos ter:
Então vamos desenhar cada uma das componentes:
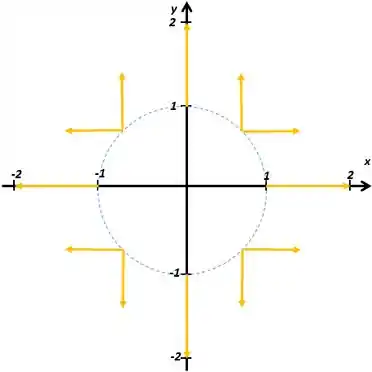
Passo 3
O nosso objetivo aqui é desenhar o campo radial, então vamos achar a resultante dessas componentes. Ficará assim:
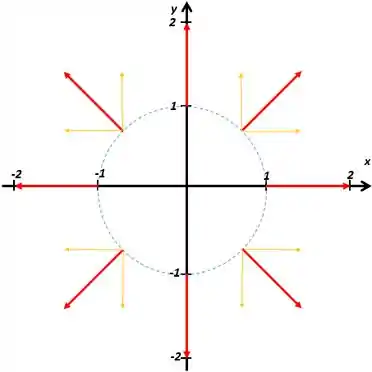
Finalmente, vamos ter os vetores definitivos, em vermelho; e as componentes, em amarelo.
Pronto, tudo feito!
Resposta