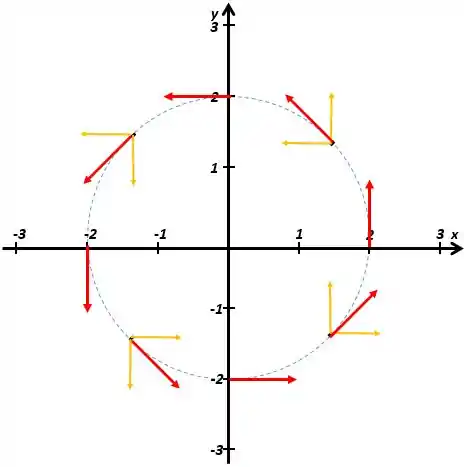
Desenhe o campo radial
Juntamente com suas componentes verticais e horizontais em um conjunto representativo de pontos da circunferência
Passo 1
O exercício pede um conjunto representativo na cicunferência , então acho que podemos escolher os pontos sobre o eixo:
E os pontos “médios”, onde e são iguais em módulo:
Por enquanto, vamos ter:
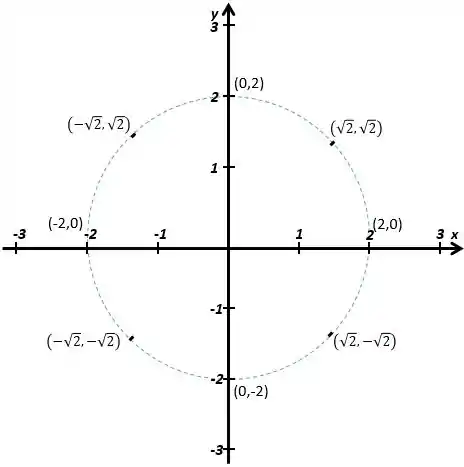
Passo 2
Agora, em cada um desses pontos, vamos traçar as componentes horizontais, dadas por , e verticais, dadas por .
Nesse caso temos
Que parece meio complicado, mas não é tanto, já que na circunferência , então basicamente temos e , o que nos dá:
Então vamos desenhar cada uma das componentes:
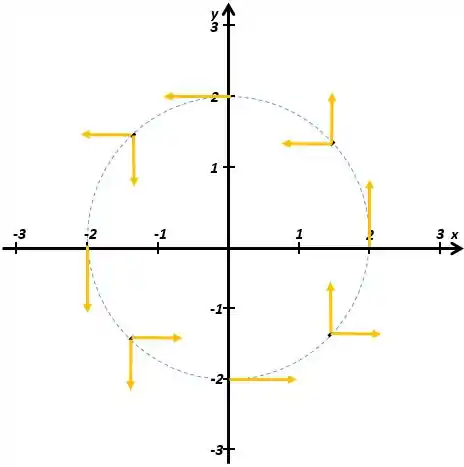
Agora é só somar as componentes e traçar o vetor final!
Passo 3
Finalmente, vamos ter os vetores definitivos, em vermelho; e as componentes, em amarelo:
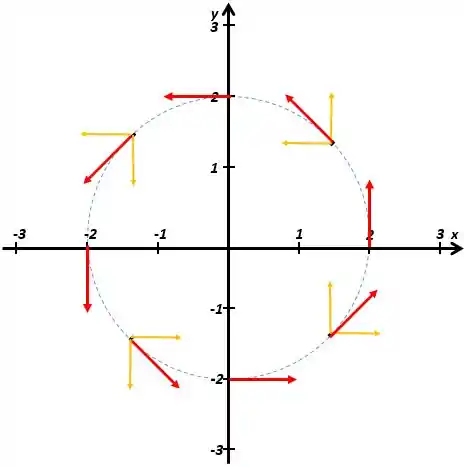
Pronto, tudo feito!
Resposta