Integral de Linha – Caso Escalar
Sejam tais que . Considere a curva representada parametricamente por ,
d) Considere os campos de vetores e . Assinale abaixo qual o gráfico de e .
Passo 1
O que temos que fazer aqui é pegar um vetor qualquer e substituir em e depois em para sabermos como fica esse gráfico.
Vamos pegar alguns pontos simples
Então, em isso vai ficar
Isso graficamente vai ficar
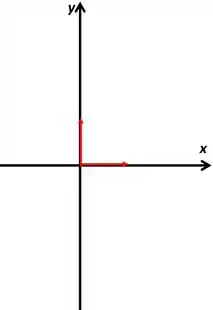
Malandramente eu peguei esses dois, porque qualquer outro que esteja no primeiro quadrante vai ser a soma desses dois caras, então podemos perceber que o gráfico de é o gráfico da direita, isso faz com que o gráfico de seja o gráfico da esquerda.
Resposta
é o gráfico da direita e é o gráfico da esquerda
Exercícios de Livros Relacionados
Calcule int_c (x - y + z - 2) d s onde C é o segmento de reta x = t , y = (1 - t) , z = 1 de (0,1 , 1) a ( 1,0 , 1 )
Sejam vec f = (x z , z y , x y) e vec g = (x^2 , y^2 , z^2) .Determinar:g) (grad xx vec f) * (grad xx vec g)
Verificar se as seguintes funções são harmônicas em algum domínio.b) f x , y = 2 x 2 - y 2 + y + 10
Verificar se o campo dado é irrotacional.c) vec f (x , y , z) = (y z e^(x y z) , x z e^(x y z) , x y e^(x y z))
Verificar se as seguintes funções são harmônicas em algum domínio.a) f x , y , z = z x + ln x y