USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 2 - 2022.1, Questão 21a
Calcule onde se
- é a curva , percorrida uma vez no sentido horário.
Passo 1
Olá meu amigo, Yuri aqui e vamos dar uma olhada na nossa curva antes de qualquer coisa.
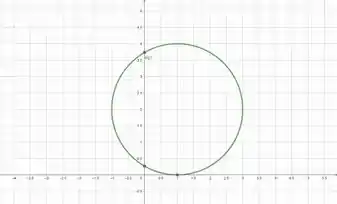
Passo 2
Para esse querido circulo como caminho, iremos utilizar o teorema de Green, então
Em que k é a região interna do circulo.
Então calculando nossa integral
Resposta
Exercícios de Livros Relacionados
Calcule int_c (x - y + z - 2) d s onde C é o segmento de reta x = t , y = (1 - t) , z = 1 de (0,1 , 1) a ( 1,0 , 1 )
Sejam vec f = (x z , z y , x y) e vec g = (x^2 , y^2 , z^2) .Determinar:g) (grad xx vec f) * (grad xx vec g)
Verificar se as seguintes funções são harmônicas em algum domínio.b) f x , y = 2 x 2 - y 2 + y + 10
Verificar se o campo dado é irrotacional.c) vec f (x , y , z) = (y z e^(x y z) , x z e^(x y z) , x y e^(x y z))
Verificar se as seguintes funções são harmônicas em algum domínio.a) f x , y , z = z x + ln x y