Calcule , onde é a parte da curva contida no semiplano orientada no sentido anti-horário.

Pelo Teorema de Green, considerando uma curva fechada orientada no sentido anti-horário e a região limitada por ela, temos:

Mas o problema pede a integral de linha na curva contida no semiplano . Ou seja, uma parábola com simetria em , que vai de a :

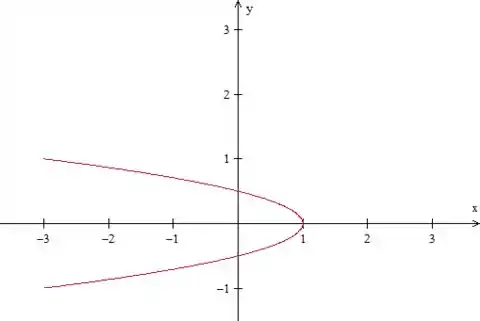
Logo, essa curva é aberta, precisamos fechar!

Então vamos fechá-la, com uma reta mesmo, que liga os pontos final e inicial, no mesmo sentido do arco:

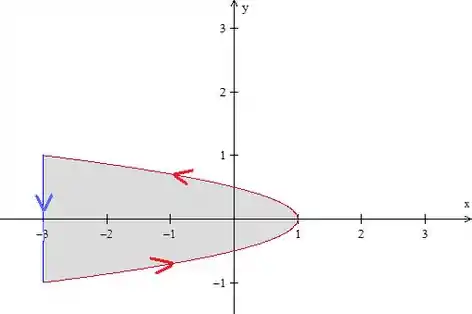
Então, sendo a união a parábola com a o segmento de reta orientados positivamente, temos:

Onde é a região em cinza na figura acima. Então, para encontrar a integral que queremos, precisamos resolver a integral dupla e a integral de linha na reta.

Repare que o campo não possui indeterminação em .

Vamos começar pela integral dupla. Descrevendo a região como tipo II, temos entre e e desde até , como podemos ver na figura. Levando para a integral, temos:

Agora vamos resolver a integral de linha no segmento de reta. Vamos começar parametrizando o segmento.

Como o segmento pertence à reta , podemos usar essa parametrização aqui:

Onde vai de a (por causa da orientação de ).

Agora vamos derivar essa parametrização:

Escrevendo o campo

Nas variáveis da parametrização, temos:

Podemos, então, substituir os valores que encontramos na fórmula abaixo:

Integral dá trabalho, né? Aqui, você pode pensar no seguinte: como essa função é ímpar (), o seu gráfico é espelhado em relação ao eixo , ou seja, toda a área que temos de a é igual à que temos de a , porém, uma integral terá sinal contrário à outra. Isso quer dizer que a integral de a será igual a zero! Logo:

Agora vamos substituir os valores que encontramos para calcular o que o problema pediu: