Questão 2: Utilize o Teorema de Green para calcular a integral de linha

Onde é o pedaço do gráfico com ponto inicial e ponto final .

Lembrete:

Como deu para perceber, essa última igualdade (do Teorema de Green), envolve uma integral dupla, e nem sempre resolver uma integral dupla é mais fácil de calcular do que uma integral de linha. Nesse caso vai ser, pois o problema já nos mandou fazer assim, mas se ele não nos tivesse pedido, bastava calcular essa subtração de derivadas parciais e ver se elas simplificam as contas:

e são componentes, do campo...

Logo...

E

Então...

Veja que essa subtração é relativamente mais bonita de simples que o próprio campo, e isso nos sugere Green, mesmo que o problema não nos falasse nada, saca?

Bem, mas para aplicar o Teorema de Green precisamos no mínimo nos certificar se o teorema de fato pode ser aplicado, neh? Esse teorema, como já deve saber, exige três condições:

1. Curva fechada que delimita a região .
2. Sem singularidades onde estamos trabalhando.
3. Curvas orientadas positivamente.

Vamos verificar cada uma a partir de agora, ok?

A começar pela curva que deve ser uma curva fechada. A nossa curva é o gráfico de:

Pra ficar mais fácil o entendimento, temos que desenhar essa curva, mas não se preocupe que vou te ajudar: veja que essa curva é de terceiro grau:

Então ela tem que ter uma cara de função cúbica :

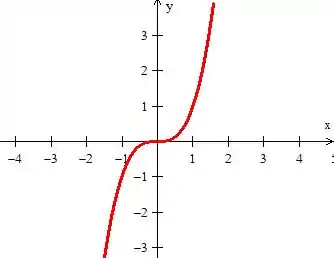
Só que calma jovem, essa ainda não é a nossa curva não, pois se você perceber na sua equação:

Ela passa por em pontos: e , então a cara da nossa curva é essa daqui oh:

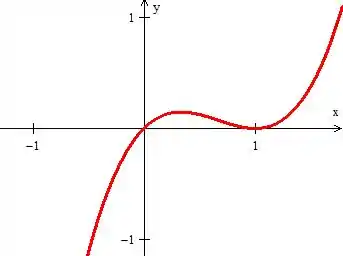
E mais! O enunciado restringe a nossa curva apenas entre esses pontos que ela corta o eixo :

“... com ponto inicial e ponto final .”

Pronto, mas já deu pra sacar que a curva é aberta, neh, e teoricamente não podemos aplicar o teorema de Green não. Mas não se preocupe que temos uma “carta na manga”: Ora, se a curva é aberta, então a fechamos com outra curva:

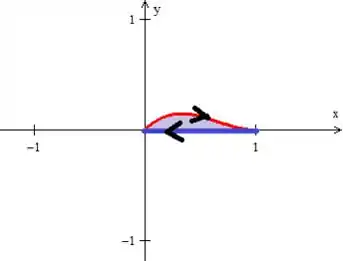
No caso pode ser essa reta passando por , mesmo. Só para não nos perdermos, vamos chamar essa reta de . AH! E com isso, temos uma região fechada por duas curvas:

A outra preocupação de Green se refere ao campo . De acordo com ele, temos que ter um campo sem singularidades onde estamos trabalhando, ou seja, sem problemas de definição:

E veja que o nosso não tem nenhum!

Por último, temos que ter uma curva girando no sentido anti-horário, para estar orientada no sentido positivo:

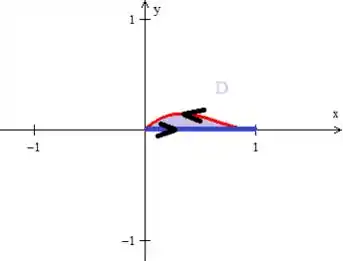
Porém, a nossa curva, originalmente está girando no sentido horário, então na igualdade de green, devemos multiplicar por a integral dupla, saca?

Assim, podemos colocar as curvas girando no sentido que a gente quer:

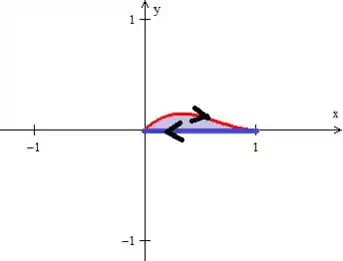
E agora estamos obedecendo também !

Com isso, sendo satisfeito, todas as condições do Teorema, podemos finalmente aplicar Green...

Como ...

O que queremos é a integral em (na curva cúbica), então devemos isola-la:

Bora calcular cada uma dessas duas integrais?

Começando pela integral dupla:

Veja que temos que descrever a região e para isso, vamos olhar pra ela mais uma vez:

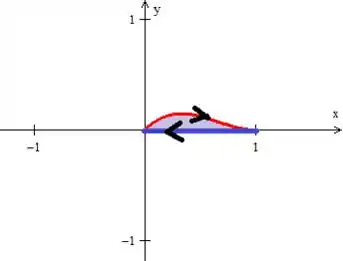
Podemos descrevê-la como região do tipo , onde o varia em um intervalo numérico bem definido:

Enquanto o varia de uma base e um teto (no caso a base é a reta e o teto é a equação cúbica):

Assim:

Isso nos sugere uma substituição simples:

Como

Então...

Agora, não podemos nos esquecer dos limites de integração...

EPA! Se os limites foram iguais, então nem precisamos terminar a conta:

Vamos agora para a última integral... A de linha:

• A primeira coisa é parametrizar a curva (que é uma reta e tem )...

Onde o parâmetro dessa reta varia de até ...

• Agora temos que ter o ...

Porém, esse aponta para a direita, sendo que nós sabemos que ele deve apontar pela esquerda...



• Devemos também, trocar os termos do campo...

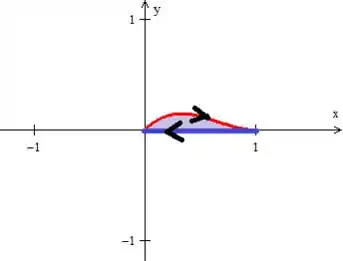
Agora é só substituir mesmo:

Beleza, voltando para a integral onde paramos, no passo :