Considere a curva parametrizada com A integral é igual a:
Passo 1
Bom, como esse campo ai não parece nada bonito de trabalhar, a gente já pensa no teorma de green até por que o método direto parece quas euqe inviável.
Para isso, temos que conferir as condições do teorema.
Primeira delas, curva fechada. Para conferir isso, vamos substituir os valores das extremidades de t na parametrização para identificar se são pontos diferentes. Se encontrarmos pontos diferentes, isso indica que estamos trabalhando com uma curva fechada.
Bom, da pra ver ai que estamos trabalhando com uma curva aberta.
Alem disso o terome nos pede campo sem singularidade e orientação positiva. Quando a isso não temos nenhum problema.
Passo 2
Uma vez conferida as condições, nosso teorema é o:
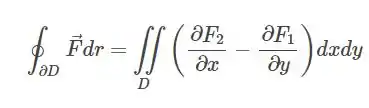
Onde será a união entre a curva e a reta que utilizaremos para fechar a curva
Então o teorema será escrito como:
Passo 3
Vamos então começar calculando a integral dupla.
Opa, isso já dá uma facilitada na nossa vida, uma vez que a integral dupla vai toda ser igual a zero.
Passo 4
Partindo agora então pra integral de linha, vamos começar parametrizando uma reta que liga os pontos (2,0) e (0,0), então vamos lembrar de mudar o sinal na integral.
Termo ds:
Campo em função da parametrização:
Montando então a integral (sem esquecer de trocar o sinal por conta do sentido de giro).
Passo 5
Voltando então ao teorema: