Seja a curva em parametrizada por
Calcule a área que fica entre a curva e o eixo .
Sugestão: aplicar o Teorema de Green, usando um campo vetorial tal que
Passo 1
Antes de tudo vamos entender que região é essa. Repare que os pontos inicial e final da curva são
Isso quer dizer que ela começa no eixo e volta para ele. Então, para termos uma região fechada, vamos criar o segmento de reta que vai de a .
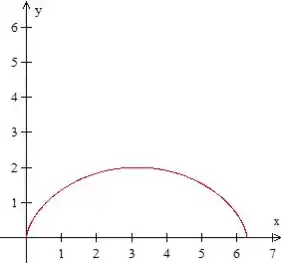
Agora repare que a curva do problema vai desde a , ou seja, ela gira no sentido horário. Para termos uma orientação positiva, então, queremos a curva oposta a essa, .
Assim, podemos aplicar o Teorema de Green:
Sendo as curvas orientadas positivamente (anti-horário)e sendo a região limitada por elas.
Passo 2
Tá, mas nós queremos a área de , e aí? Vamos forçar isso a aparecer encontrando um campo (como sugere a questão) tal que
Pode ser
Isso nos dá
Passo 3
Agora precisamos resolver essas integrais de linha. Começando pela curva do problema: como ela já está parametrizada, o próximo passo é derivar essa parametrização.
Agora a gente usa a fórmula
Temos
O que nos dá
Passo 4
Agora, precisamos da integral no segmento que vai de a . Como o segmento pertence à reta , podemos parametrizá-lo assim:
Onde .
Derivando isso aí
Agora, vamos usar a fórmula
O que nos dá
Passo 5
Temos então