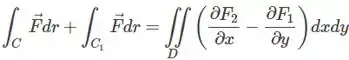Seja o trecho da elipse com , de (2,0) a (0,0). A integral é igual a:
Passo 1
Bom, pra começar essa questão, vamos ver essa elipse do enunciado.
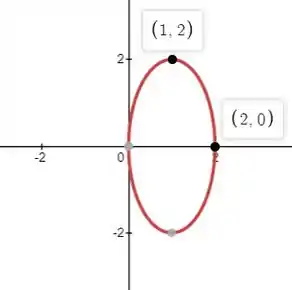
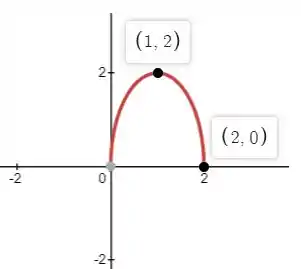
No então ele que apenas o , logo ficamos com:
Passo 2
Essa parece uma questão ideal para aplicarmos o teorema de green, no entanto, se você for observar, logo de cara temos uma curva aberta. Pra esse caso vamos simplesmente fechar essa curva com uma . Assim, nosso teorema fica:
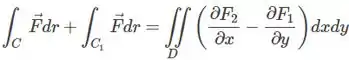
Passo 3
Resolvendo primeiro a integral fupla ficamos com:
Ficamos então com:
Isso nos da exatamente 2 vezes a área da região, que se você for observar é a metade da elipse. Logo ficamos com:
Passo 4
Resolvemos então a integral dupla. Ficamos agora precisando da integral de linha em cima da nova curva que precisamos usar para fechar a curva . Recomendo usar sempre a mais simples possível. Pra esse caso pode ser simplesmente uma reta que passa por cima do eixo x, ligando os pontos (0,0) e (2,0).
Parametrizando:
Precisamos agora da derivada da parametrização:
E finalmente do campo em função da parametrização. Lembrando que nosso campo era , ficamos com:
Passo 5
Podemos então finalmente montar a integral e resolvê-la.
Passo 6
Por último, mas não menos importante, precisamos voltar ao teorema de green.