Usando o Teorema de Green, calcular
Onde é o campo vetorial e é a curva por partes formada por e , , que vai do ponto ao ponto .
Passo 1
Ele diz para gente usar o teorema de Green para calcular uma integral de linha vetorial sobre a curva .
Andando por ela, a gente começa em , passa pela reta , até a origem (a interseção entre e ) e depois vai pela reta , até . Esboçando esse caminho:
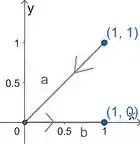
Então é esse caminho que a gente desenhou.
Passo 2
O Teorema de Green diz que a gente pode calcular a integral de em uma curva por essa relação:
Onde é uma região e é a curva fronteira dessa região. Só que ele tem umas condições para aplicar.
Primeira condição: A nossa região precisa ser fechada: Repara que não é uma curva fechada, a gente vai precisar fechar ela. O jeito mais simples é fechar ela com um segmento de reta contido em .
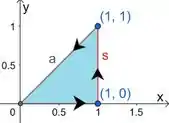
Vamos chamar ele , e parametriza-lo assim:
Repara que a gente parametrizou ele no sentido que casa direitinho com o sentido da nossa curva . Nossa fronteira agora é formada por e .
Por isso, podemos reescrever o lado esquerdo do teorema assim
Passo 3
Segunda condição: A fronteira precisa ser percorrida no sentido positivo: Que sentido é esse? É só você imaginar que está andando na borda no sentido das setinhas, sua região precisa está à sua esquerda.
Repara que isso acontece na nossa região limitada por e . Então essa está tranquila!
Terceira condição: não pode ter descontinuidades dentro da nossa região. Aí a gente olha para o nosso :
Ela realmente está bem definida para todo . Então essa tá tranquilo também. Bora lá aplicar o Teorema!
Passo 4
Substituindo nele as coisas que a gente tem:
Bora calcular esse integrando ali:
A ideia é calcular o valor da integral de linha sobre calculando essa integral dupla na direita e a outra integral de linha em .
Passo 5
Vamos olhar para integral dupla
é o nosso triângulo limitado por e . Aí a gente precisa definir os extremos de integração para percorrer ele.
No eixo , vemos que ele está entre:
Já no eixo , ele é limitado por baixo por e por cima pela reta que passa por e . Achando a equação dessa reta, vemos que ela é
Aí dizemos que:
Nossa integral fica:
Calculando ela:
Passo 6
Vamos olhar para integral de linha:
A fórmulinha para montar ela é
O intervalo é o domínio do segmento , no caso, .
O termo é quando a gente substitui as componentes de em :
Aí o campo fica:
E é a derivada de :
Substituindo essas coisas na fórmulinha e calculando:
Passo 7
Substituindo o que a gente achou na nossa expressão para a integral de linha sobre :