Questão 3: Seja o campo
E o arco da curva de até . Usando o Teorema de Green calcular
Passo 1
Normalmente, podemos resolver integrais de linha de uma forma direta calculando essa integral:
Agora poxa! Você já deve ter notado que esse campo é muito chato para trabalharmos com ele direto dessa forma, até porque teríamos que substituir no campo e ia aparecer algo do tipo . Mas não se preocupe, pra isso que serve o teorema de Green (pedido no problema):
Ou seja, estamos prestes trocar essa integral de linha por uma integral dupla ! (não se preocupe com a notação que isso só significa borda da região )
Passo 2
Mas mesmo que o problema não nos tivesse mandado seguir e você estiver em dúvida como resolver, sugiro que calcule essa subtração de derivadas parciais, como vamos fazer agora:
Derivando então...
Calculando então a outra derivada parcial...
Então...
POW! Que resultado, bonito, não é verdade. Isso é a prova “viva” que vamos utilizar mesmo o Teorema de Green, pois ele vai mesmo simplificar as nossas contas ;)
Passo 3
Todavia, para aplicar o Teorema de Green precisamos no mínimo nos certificar se o teorema de fato pode ser aplicado, neh? Esse teorema, como já deve saber, exige três condições:
- Curva fechada que delimita a região .
- Curvas orientadas positivamente.
- Sem singularidades onde estamos trabalhando.
Vamos verificar cada uma a partir de agora, ok?
Passo 4
A começar pela primeira: uma curva fechada. Isso é um pequeno problema pra gente, já que a nossa curva é esse pedaço de cossenoide aqui, veja:
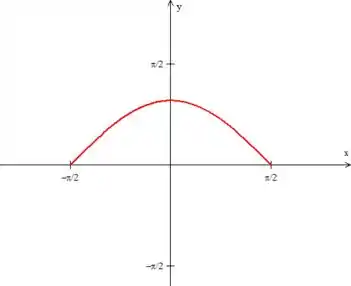
Mas calma! Esse problema pra gente pode ser facilmente resolvido fechando a curva com a curva mais simples que conseguirmos (que nesse caso é essa reta azul aqui no eixo ):
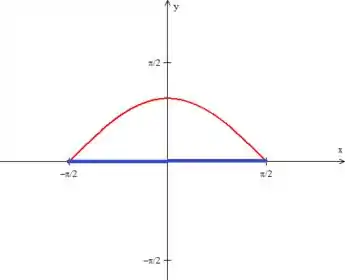
Não se preocupe que o Teorema de Green nos dá total liberdade para fazermos isso. A propósito, vou chamar essa curva de .
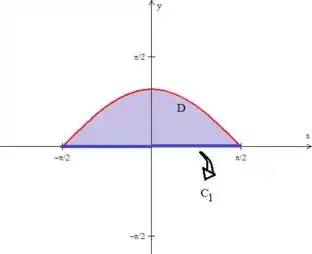
Vale dar uma ressaltada aqui também, que o a borda da região fechada , agora é composta por duas curvas: e ...
Passo 5
Show, curva escolhidas, podemos verificar se ambas giram no sentido positivo, lembrando que para isso acontecer, devemos ter ambas as curvas girando no sentido anti-horário:
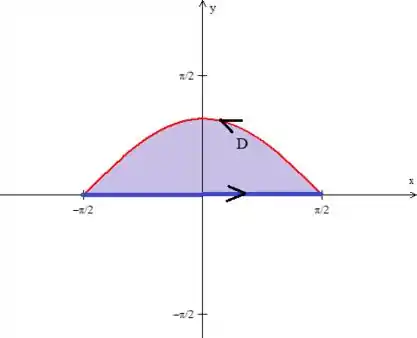
Mas calma lá, jovem! Se você der uma olhada com atenção para o enunciado do problema, queremos calcular a integral na curva (a cossenoide) de até . Então ambas as curvas estão girando naturalmente nesse sentido aqui:
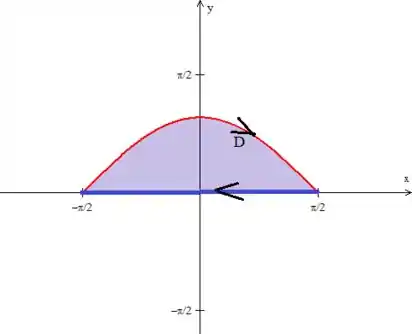
Para evitar problemas com Green, então, coloquemos um sinal negativo em frente a integral dupla:
E agora, ao invés de trabalharmos com a curva girando para o anti-horário, como Green exige, podemos usar a rotação original (o sentido horário):
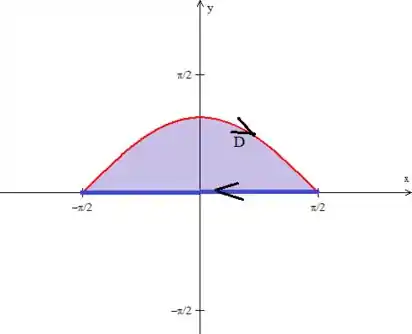
Passo 6
Por último, podemos verificar a última exigência do teorema que é saber se o campo tem algum problema de definição em algum ponto:
Como é composto por exponenciais e polinômios, então não tem o que temer não: ele não tem singularidade alguma !
Passo 7
Com três essas coisas funcionando perfeitamente em harmonia, podemos retornar para a igualdade de Green que vamos usar:
E ajusta-la!
Como , podemos separar a integral de linha:
Como, desde o início, queríamos encontrar o valor da integral de linha em cima da cossenoide (curva ), podemos isola-la:
Outra coisa que poderíamos fazer aqui para facilitar o cálculo é: consegue ver que a integral em cima de está negativa? Podemos inverter o sinal se trocarmos o sentido de giro!
É a mesma coisa, só que agora, ao invés da curva girar para trás, como vimos no final do passo , ele deve andar para frente:
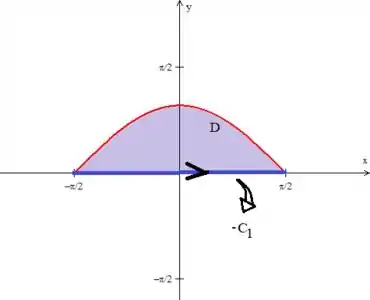
Mais uma vez, não se preocupe que é só uma notação para indicar que a curva gira no sentido oposto .
Passo 8
Tá, vamos começar resolvendo a integral dupla:
Precisamos então descrever a região :
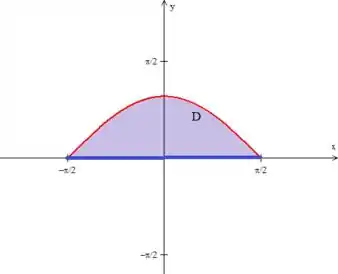
O que pode ser feito com o auxílio de região do tipo 1, onde podemos ter o variando entre números:
Enquanto o varia de uma base até um teto:
Logo...
Resolvendo a integral dupla:
A primeira integral, vamos ter de calcular com integração por partes:
Onde (pois é fácil de derivar) enquanto ...
Para outra integral:
Basta lembrar de que ...
Assim:
Passo 9
Calma Jovem! Ainda não acabou não, pois nos falta a integral de linha:
Onde vamos:
- Parametrizar a curva :
- Encontrar o termo ...
- Encontrar o campo nos termos da parametrização:
Onde está variando de:
Agora é só substituir na integral de linha:
Passo 10
Finalmente podemos regressar à integral que queremos de fato encontrar o valor: