Calcule a integral de linha do campo vetorial
sobre a curva parametrizada por , onde .
Passo 1
Pela parametrização observamos que
Por coordenadas elípticas, percebemos que a equação cartesiana seria
Passo 2
Agora, imagina comigo jogar a parametrização dentro daquele campo bizarro ali...complicado, né? Por isso a gente já pensa no Teorema de Green, onde vamos trocar essa integral de linha por uma integral dupla, dentro dessa região que acabamos de obter a equação cartesiana, tranquilo?
No entanto, uma da condições do teorema de green é que tenhamos curva fechada. Observa que estamos trabalhando com a metade da direita de uma elipse
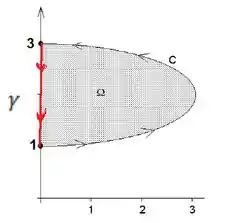
Por essa razão vamos fechar a curva com essa reta vermelha que chamarei de (se atentando para manter a orientação positiva)
Passo 3
Parametrizando essa curva ficamos com
No entanto, observe que na hora de montarmos a integral, temos que lembrar de trocar o sinal, uma vez que a curva roda de 3 para 1, e não no sentindo da parametrização.
Passo 4
Bom, voltando pra o Teorema de green ficamos então com
Resolvendo primeiro a parte da integral dupla, calculando , encontramos 2 como resultado:
Substituindo encontramos:
Ficamos então com
Resolvendo a integral de linha, uma vez que o campo é
E a parametrização é
Observa que falei que não importa o que entra ali naquela parte... but why? Quando formos multiplicar com a derivada da parametrização, aquele termo some. Observa que
Então vamos ficar com
Agora temos de lembrar de trocar o sinal para conservar a orientação positiva, então ficamos com
Passo 5
Retornando para a integral dupla, ficamos agora com:
Observa pela nossa figura acima que estamos trabalhando com a metade de uma elipse, que é dada por
Agora dividido por 2, por ser a metade apenas.
Passo 6
Pra fechar então voltamos ao teorema pra juntar os valores que obtivemos.