Sejam o campo vetorial plano definido por e a curva regular dada pela equação e a desigualdade
Orientada indo do ponto ao ponto
a) Esboce
b) Determine uma parametrização da curva regular que é o segmento de reta que liga os pontos e .
c) Use o teorema de Green para calcular a integral
(Dica: Use a concatenação de do item (b), para obter a curva fechada simples.)
Passo 1
Letra a)
Vamos começar com a equação
Na forma que ela tá, igualando para descobrir as raízes vamos ter:
Se abrirmos essa equação fica fácil ver que se trata de uma equação do segundo grau com concavidade para baixo
Podemos marcar também o ponto máximo, que se dá quando está metade entre as duas raízes
A coordenada então é
Podemos agora marcar a parábola que passa por esses pontos
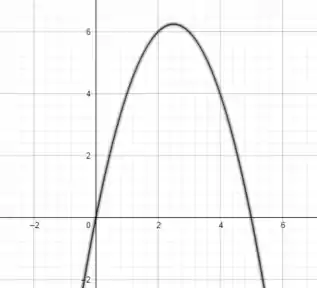
Passo 2
Olhando a outra equação é a região acima da reta
Igualando a reta à parábola saberemos que os pontos de intersecção são
Substiuindo na equação da reta que é mais fácil os pontos são
Juntando as duas regiões temos
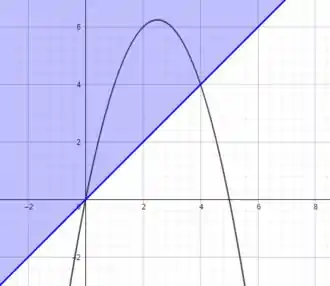
Então a curva do problema vai ser só essa parte que está acima da reta
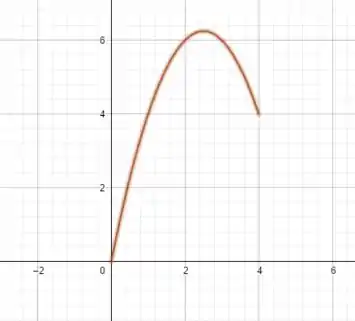
Passo 3
Letra b)
Nós já sabemos que a reta que passa por esses pontos é a reta
Uma parametrização para a reta é a seguinte
Agora como queremos um segmento de reta que liga os pontos e , vamos fazer o t variar de a
Passo 4
Letra c)
O teorema de Green relaciona a integral de linha de uma curva fechada com a integral dupla sobre a área limitada por essa curva.
Temos a fórmula que é a seguinte:
Aqui atenção que na representação, é a área da região enquanto que é o contorno dessa região.
A integral da esquerda é a soma das integrais de linha de cada curva, então podemos escrever
Temos que ficar atentos à orientação da curva fechada que deve ser anti-horária. A curva , esta no sentido correto, agora para precisamos que o sentido dela seja indo de (4,4) para (0,0).
Imagem
O que fazemos então para conserta isso é colocar
significa que a minha curva está orientada no sentido contrário ao que está parametrizada e para a nossa integral isso significa
Passo 5
Queremos encontrar a integral de linha de na curva
Da expressão do teorema de Green
Manipulando vamos ter:
Vamos calcular agora a integral dupla.
Sendo , vamos ter:
Para o domínio vamos considerar que ela é uma região do tipo . A variável varia entre constantes e a variável varia entre funções
Em a região varia entre e :
Em a região varia da reta até a reta :
Resolvendo agora a integral dupla:
Resolvendo para :
Resolvendo agora para :
Passo 6
Vamos agora calcular para a integral de linha de
Calculando
Calculando
Aplicando o produto escalar:
Resolvendo essa integral para :
Voltando para o calculo da integral de linha
Substituindo o que a gente calculou:
Passo 7
Resposta
a) 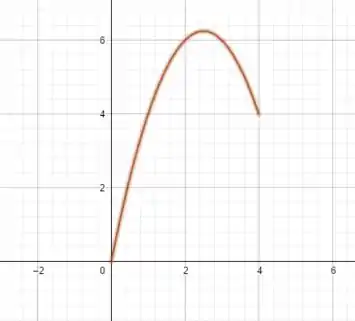
b)
c)