Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas Abertas

Ver Teoria
Exercício 21123456789101112131415161718192022232425262728293031323334353637383940414243

Enunciado

Questão 3: Seja

F → = - y 3 3 - 2 y e x - y ,   2 y - 1   e x - y + x 3 3 + 1

Calcule ∫ γ   F → ⋅ d r → , onde γ é o semicírculo dado por x 2 + y 2 = 4 , y ≥ x , e percorrido de - 2 , -   2 até 2 , 2 .

Passo 1

Bem, para termos uma noção clara de como vamos resolver essa integral de linha, primeiro vamos fazer um esboço dessa curva γ ...

O próprio problema nos disse que ela é a parte da circunferência de raio 2 ...

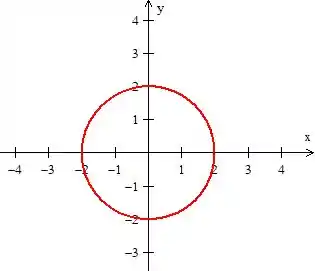
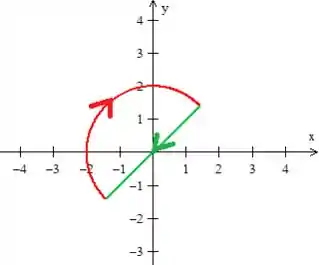
Mas só queremos a parte acima da reta y = x (digo acima, pois ele indicou y ≥ x ):

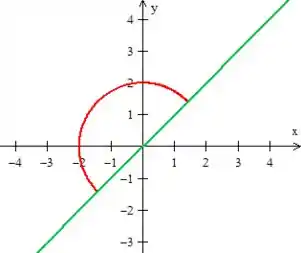
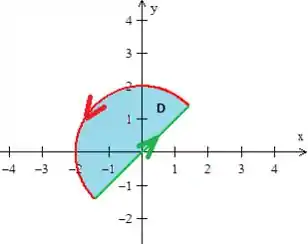
Logo, essa é a curva que queremos é essa parte vermelha aqui (não se esqueça de colocar a orientação pedida):

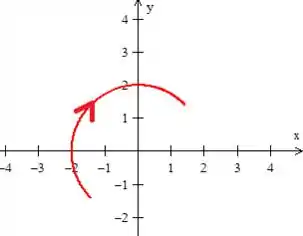
Passo 2

Bem, estamos trabalhando em cima de uma circunferência e, além disso, o campo F → não é nada elegante. Duas indicações de que devemos usar o Teorema de Green. Para termos certeza, calculemos:

∂ F 2 ∂ x - ∂ F 1 ∂ y

Como...

F → = - y 3 3 - 2 y e x - y ⏟ F 1 ,   2 y - 1   e x - y + x 3 3 + 1 ⏟ F 2

Então...

∂ F 2 ∂ x = ∂ 2 y - 1   e x - y + x 3 3 + 1   ∂ x =

2 y - 1   e x - y ⋅ 1 + x 2

E

∂ F 1 ∂ y = ∂ - y 3 3 - 2 y e x - y ∂ y =

Cuidado com a regra do produto aí, heim...

- y 2 + ∂ - 2 y ∂ y e x - y + ∂ e x - y ∂ y - 2 y =

e cuidado coma regra da cadeia também...

- y 2 - 2 e x - y + e x - y ⋅ - 1 - 2 y =

- y 2 - 2 e x - y + 2 y e x - y =

- y 2 + 2 e x - y y - 1

Subtraindo então...

∂ F 2 ∂ x - ∂ F 1 ∂ y = 2 y - 1   e x - y + x 2 - - y 2 + 2 e x - y y - 1 =

∂ F 2 ∂ x - ∂ F 1 ∂ y = x 2 + y 2

Subtração bem easy! Então estamos mesmo lidando com Green :D

Passo 3

O teorema de Green nada mais é do que essa famosa igualdade:

∫ ∂ D   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Onde esse ∂ D é a borda da região fechada D , saca?

Bem, mas é claro que não podemos aplicar essa igualdade assim... Do nada. Precisamos analisar as condições do teorema:

1º - Temos que ter uma curva fechada ∂ D delimitando D .

2º - deve estar orienta positivamente!

3º - Precisamos de um campo sem singularidades onde estamos trabalhando.

Vamos ver se no nosso caso, cada um desses itens é satisfeito? Então me acompanhe! :D

Passo 4

1º - Temos que ter uma curva fechada delimitando D .

Como pode perceber, a nossa não é fechada:

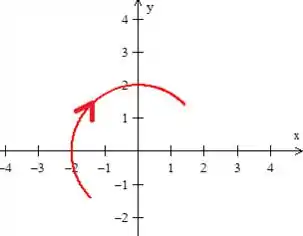
Mas podemos fecha-la com a própria reta y = x , verdinha que vamos nomear de C ...

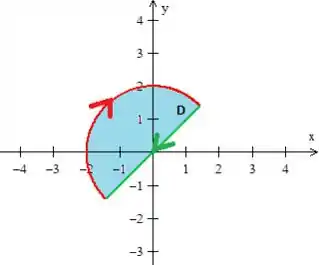
Como a borda ∂ D no nosso caso é a junção de duas curvas...

∫ ∂ D   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A     →

∫ - γ   F → ⋅ d r → + ∫ C   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Repare que a curva γ está com um sinal negativo, isso porque a curva...

Passo 5

2º - deve estar orienta positivamente!

Isso significa que o conjunto tem que estar girando no sentido anti-horário:

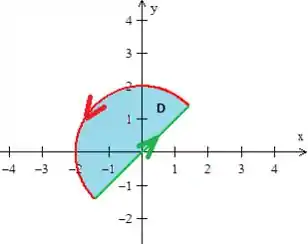
Como a curva γ não está, invertemos o seu sinal, saca? Mas, esse sinal pode sumir, se invertemos o sinal da integral de linha dela...

∫ - γ   F → ⋅ d r → + ∫ C   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A     →

- ∫ γ   F → ⋅ d r → + ∫ C   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Passo 6

3º - Precisamos de um campo sem singularidades onde estamos trabalhando:

O que já acontece com o nosso campo...

F → = - y 3 3 - 2 y e x - y ,   2 y - 1   e x - y + x 3 3 + 1

Passo 7

Aplicar o teorema!

- ∫ γ   F → ⋅ d r → + ∫ C   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

- ∫ γ   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A - ∫ C   F → ⋅ d r →

∫ γ   F → ⋅ d r → = ∫ C   F → ⋅ d r → - ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Se queremos essa integral de linha sobre a curva γ , calculemos essas duas outras integrais desse lado direito e vamos ser felizes !

Passo 8

Primeiro a integral dupla...

∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A =

∬ D   x 2 + y 2 d A

Como estamos trabalhando em uma região circular e envolvendo soma de coisas ao quadrado... Usemos as coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

e sabemos que...

x 2 + y 2 = r 2

Para a variação de r , verificamos que ele sai da origem e vai até a borda vermelha de raio 2 ...

0 ≤ r ≤ 2

Quanto ao θ ...

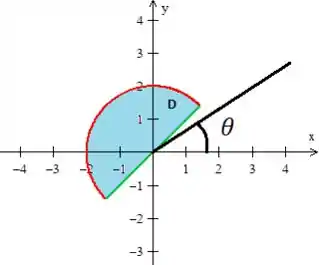
Ele entra na reta y = x e sai pela mesma reta, então... Substituindo as polares nessa reta...

r cos ⁡ θ = r sin ⁡ θ   →

cos ⁡ θ = sin ⁡ θ   →  

sin ⁡ θ cos ⁡ θ = 1   →

tan ⁡ θ = 1

Então θ só pode estar saindo de 45 ° e indo até 180 ° + 45 ° que são os ângulos que satisfazem a condição dessa tangente...

π 4 ≤ θ ≤ 5 π 4

Passo 9

Substituindo então na integral dupla...

∬ D   x 2 + y 2 d A =

Não se esqueça do Jacobiano:

∫ π 4 5 π 4 ∫ 0 2 r 2 ⋅ r   d r d θ =

∫ π 4 5 π 4 ∫ 0 2 r 3   d r d θ =

∫ π 4 5 π 4 ∫ 0 2 r 3   d r d θ =

∫ π 4 5 π 4 r 4 4 0 2 d θ =

∫ π 4 5 π 4 16 4   d θ = 4 ∫ π 4 5 π 4   d θ

4 5 π 4 - π 4 = 4 π

Passo 10

Vamos agora calcular essa integral de linha que apareceu:

∫ C   F → ⋅ d r →

Ela é a integral de linha sobre essa reta verde:

A primeira coisa que devemos fazer aqui é parametrizar essa reta, o que pode ser feito utilizando uma parametrização explícita:

x = t

então, como y = x ...

y = t

A curva parametrizada de uma forma legal é...

γ t = t ,   t

Como a curva gira de - 2 , -   2 até 2 , 2 ...

- 2 ≤ t ≤ 2

Passo 11

Para o termo d r → , calculemos:

d r → = γ ' t d t

Calculando a derivada...

γ t = t ,   t     →           γ ' t = 1 ,   1

logo...

d r → = 1 ,   1 d t

Passo 12

Não podemos de deixar de passar o campo vetorial para os termos da parametrização:

F → = - y 3 3 - 2 y e x - y ,   2 y - 1   e x - y + x 3 3 + 1

Como x = t e y = t ...

F → = - t 3 3 - 2 t e 0 ,   2 t - 1   e 0 + t 3 3 + 1

F → = - t 3 3 - 2 t ,   2 t - 1   + t 3 3 + 1

F → = - t 3 3 - 2 t ,   2 t   + t 3 3 - 1

Passo 13

Voltando para a integral de linha...

∫ C   F → ⋅ d r →

e substituindo esses caras que acabamos de encontrar:

∫ - 2 2 - t 3 3 - 2 t ,   2 t   + t 3 3 - 1 ⋅ 1 ,   1 d t =

Calculando esse produto interno:

∫ - 2 2 - t 3 3 - 2 t +   2 t   + t 3 3 - 1   d t =

∫ - 2 2 - 1   d t =

- 2 - - 2 = - 2 2

Passo 14

Retornando ao teorema, e calma que já está acabando...

∫ γ   F → ⋅ d r → = ∫ C   F → ⋅ d r → - ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

e substituindo os resultados auxiliares...

∫ γ   F → ⋅ d r → = - 2 2 - 4 π

Resposta

- 2 2 - 4 π

Exercícios de Livros Relacionados

Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = x + y 3 , x 2 + y C consiste no arco da curva y = sen ⁡ x de ( 0,0 ) a ( 0 ,
f ( x , y ) = (x + y^2) // sqrt(1 + x^2) , C : y = x^2 // 2 entre ( 1,1 // 2 ) e ( 0,0 )
f ( x , y ) = x^3 // y , C : y = x^2 // 2 , 0 = x = 2