Sejam e a curva com . Então é
Escolha uma:
a)
b)
c)
d)
e)
Passo 1
Cara, esse campo é muito feio e a curva também é estranha. Então vamos ver se é uma boa usar o Teorema de Green. Para testar isso, vamos calcular o rotacional desse campo
Nosso campo é
Aí o rotacional fica
Nossa, ficou super simples, né? Então, bora de Green!
Passo 2
O Teorema de Green diz que a gente pode calcular a integral de em uma curva por essa relação:
Onde é uma região e é a curva fronteira dessa região. Só que ele tem umas condições para aplicar.
Primeira condição: A nossa região precisa ser fechada: Vamos esboçar nossa curva para olhar isso
Como daí a gente tem , podemos dizer que
Sendo que . Aí para esboçar isso, a gente reescreve essa equação como duas retas, uma para e outra para .
Esboçando esses dois segmentos no mesmo plano
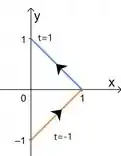
Essas setinhas representam que nossa curva sai de e vai até .
Repara que não é uma curva fechada, a gente vai precisar fechar ela. E agora?
Passo 3
O jeito mais simples é fechar ela com um segmento de reta contido em .
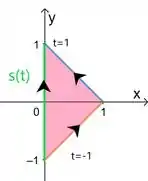
Vamos chamar ele , e parametriza-lo assim:
Nossa fronteira agora é formada por e .
Passo 4
Segunda condição: A fronteira precisa ser percorrida no sentido positivo: Que sentido é esse? É só você imaginar que está andando na borda no sentido das setinhas, sua região precisa está à sua esquerda.
Repara que isso acontece na nossa região quando andamos por cima de , mas não acontece quando andamos por cima de . Aí o que a gente faz? Desiste?! Não!
A gente pode lembrar que
Então, a gente só precisa mudar o sinal da integral de linha que representa esse segmento. Aí fica tranquilo!
Aí, podemos reescrever o lado esquerdo do teorema assim
Terceira condição: e suas derivadas não podem ter descontinuidades dentro da nossa região. Aí a gente olha para o nosso :
Ele realmente está bem definido para todo . Então essa tá tranquilo também. Bora lá aplicar o Teorema!
Passo 5
Substituindo nele as coisas que a gente tem:
Vimos que :
Repara que temos ali uma integra dupla com integrando igual a 1, isso quer dizer que a gente só precisa calcular a área de . Como é um triângulo (o rosinha) de base 2 e altura 1.
Aí temos
A ideia é calcular o valor da integral de linha sobre calculando essa integral de linha em e somando 1.
Passo 6
Vamos olhar para integral de linha:
A fórmulinha para montar ela é
O intervalo é o domínio do segmento , no caso, .
O termo é quando a gente substitui as componentes de em :
Aí o campo fica:
E é a derivada de :
Substituindo essas coisas na fórmulinha e calculando:
Passo 7
Substituindo o que a gente achou na nossa expressão para a integral de linha sobre :
Resposta
Letra a