Calcule a integral de linha
Onde é a parte da curva , que se encontra entre e , orientada de modo que é o seu ponto inicial, e
Passo 1
Bem, com um campo desse a integral parece meio inviável de se calcular pela definição, né?
Mas com Green as coisas devem simplificar bastante, já que:
Só que pra podermos aplicar o teorema, temos que garantir que a curva é fechada. Vamos ver:
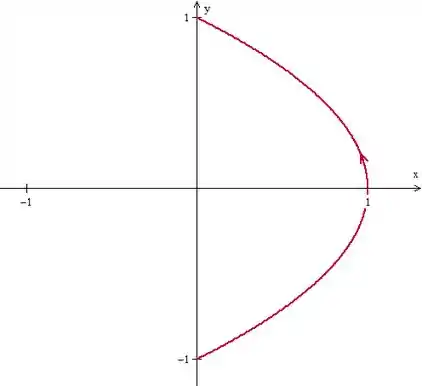
Bem, dá pra ver que nesse pedaço que ele quer, que é entre e , a curva não é fechada.
Então vamos ter que fechar a curva. Podemos simplesmente criar a reta que liga o ponto ao , ficando com algo assim:
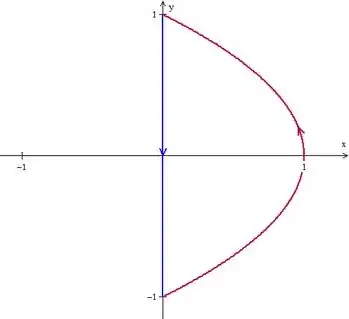
E agora sim podemos aplicar Green nessa região fechada, já orientada positivamente:
Então, para acharmos a integral sobre , vamos fazer:
Eita, mas ai vamos ter que calcular uma integral de linha pela definição de qualquer jeito, né?
Mas calma, que agora temos uma reta de , o que deve simplificar bastante as coisas, já é bem melhor do que tinhamos antes. Então vamos logo às contas!
Passo 2
Vamos começar pela integral dupla lá, que vimos que o termo é bem tranquilo:
A região é bem tranquila também:
Então, vamos ter:
Tranquilo, vamos ver a integral de linha agora!
Passo 3
Só tá faltando aquela integral de linha sobre , que vamos calcula rpela fómula mesmo:
Então primeiro de tudo precisamos da parametrização. Como temos uma reta com , é algo bem simples, só fica ligado na orientação, pois a curva precisa ir de a , e nao o contrário. Mas então vamos ter:
O vetor tangente também é tranquilinho:
E aquele campo bizarro do início da questão fica simplesmente:
Super de boa, né? Agora é só calcular!
Passo 4
Vamos jogar tudo na fórmula:
Super tranquilo também!
Passo 5
Agora que ja temos tudo, é só jogar na relação que tinhamos lá em cima:
Um resultado até simpático, eu diria... haha