4) Seja o hemisfério superior da circunferência , percorrida com ponto inicial e ponto final . O valor da integral de linha é:
Passo 1
Para resolver essa integral de linha, como podemos utilizar o teorema de Green, já o campo não tem singularidades, e a famosa subtração...
Como e ...
Passo 2
O teorema de Green nos fala...
As exigências do teorema são de que:
1º - Ter uma região fechada e delimitando uma borda . Se desenharmos a semicircunferência como manda o enunciado
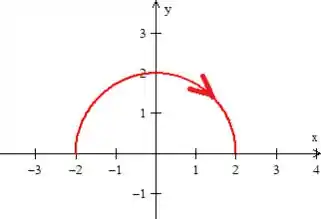
percebemos que estamos lidando com uma curva aberta. Para fecha-la, vamos pegar esse segmento de reta paralela ao , passando por :
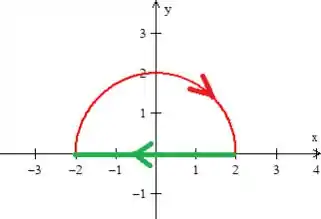
2º - O campo não pode ter singularidades. ok!
3º - As curvas devem estar girando no sentido anti-horário. Infelizmente isso não acontece então no teorema, vamos multiplicar a integral dupla por ...
Passo 3
Exigências sendo cumpridas, podemos aplicar essa igualdade:
Repare que a borda da região é composta pela curva pela curva que adicionamos...
Se queremos a integral em ...
Como , gira no sentido:
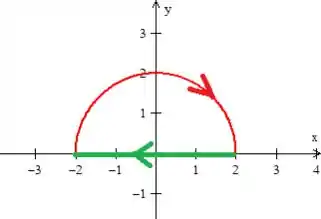
Podemos inverter isso se...
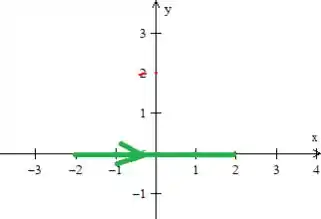
Prontinho! Basta calcular essa integral em cima de (O segmento de reta girando no sentido de para )
Passo 4
Para calcularmos essa integral, parametrizamos a curva ...
Como e varia do ponto para ...
Agora, encontremos a derivada da parametrização...
Por último, substituir os termos da parametrização no campo de vetores...