Questão 4: Utilize o Teorema de Green para calcular
Onde é o arco da circunferência , no primeiro quadrante, orientado no sentindo anti-horário.
Passo 1
Bem, antes do começarmos qualquer coisa, vamos colocar essa integral de linha de uma forma mais elegante.
Como você já pode notar, a integral de linha está assim , certo? Só que esse formato é apenas outra forma de falar que estamos trabalhando uma integral de linha de um campo de vetores:
Onde esse é o vetor...
Temos que resolver o problema utilizando Green, mas para você ter certeza se é Green ou não, sempre indico calcular essa subtração de Green:
Vamos nessa?
Passo 2
As derivadas parciais são...
logo
De fato é muito simples essa subtração nos indicando que de fato estamos lidando com Green
Passo 3
O teorema de Green nada mais é do que essa igualdade mara entre a integral de linha com uma integral dupla:
Mas antes de aplicarmos essa igualdade maravilhosa do Teorema, temos que avalizar as condições de Green, que sempre nos exige:
1º - Uma curva fechada delimitando a região .
2º - A curva , orientada positivamente.
3º - Um campo sem singularidades onde estamos trabalhando.
Vamos averiguar?
Passo 4
1º - Precisamos de uma curva fechada e delimitando uma região . Ora, a curva , pelo próprio enunciado, é uma circunferência de raio ...
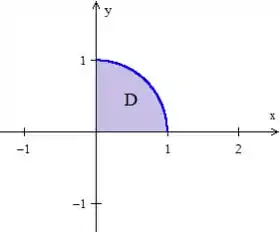
2º - E mais, ela está orientada positivamente sim! O problema nos disse que ela gira no sentido anti-horário (que é a mesma coisa):
3º - O campo que estamos trabalhando...
Não tem um problema em nenhum lugar, o que nos garante que ele já está sem singularidades !
Passo 5
Condições do Teorema sendo satisfeitas, podemos aplicar a igualdade numa boa:
Só observa que a borda da região é formada pela curva azul () e pelas duas retas do eixo que vou nomear de e :
Se queremos a integral de linha em , calculemos a integral dupla e as demais integrais de linha e beijinho no ombro ;)
Passo 6
Substituindo...
Epa! O que é uma integral dupla de ? sim! É a área da região
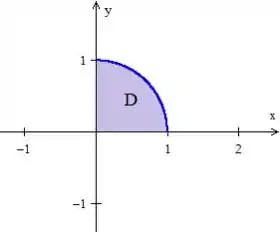
Como o raio é ...
Passo 7
Agora calculemos as outras duas integrais de linha em cima dos eixos:
é a retinha em cima do eixo :
Onde
Calculando a integral em cima de (a retinha em cima do eixo y):
Onde varia de até :
Assim olhando pelo teorema...