Teorema de Green, Integrais de linha – caso vetorial
Calcule a integral de linha , onde é o arco de elipse com , orientada de a .
Passo 1
Para escrever a curva na forma paramétrica teríamos que usar senos e cossenos, o que tornaria a integral muito complicada. Portanto, calcular essa integral pela definição está fora de cogitação! Vamos tentar usar o Teorema de Green aqui então.
O campo vetorial da questão pode ser escrito como
Vamos agora calcular :
Essa é uma expressão simples, quer dizer que estamos no caminho certo!
Passo 2
Beleza, vamos aplicar Green então, mas em que região? Precisamos fechar o arco da elipse de alguma forma, vamos tentar o mais simples: uma reta:
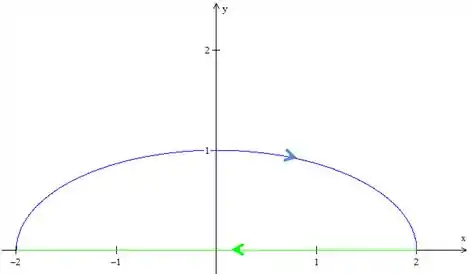
Cuidado com a orientação das curvas. O arco de elipse está com a orientação trocada, então vamos fazê-lo com a orientação de para e depois é só trocar o sinal. O novo gráfico vai ficar
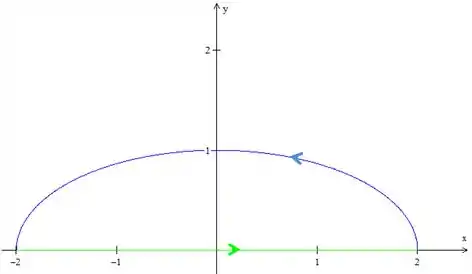
Agora podemos aplicar Green:
Onde é a reta do desenho que vai de à e é a região entre a elipse e a reta.
Eu coloquei aquele na integral de porque estamos fazendo com a orientação trocada ao pedido no enunciado.
Passo 3
Como a região está compreendida entre um arco de elipse e uma reta, a melhor saída aqui são as coordenadas elípticas. Faremos:
Pelo próprio gráfico, vemos que , o que equivale a de elipse. Os valores de variam entre a origem e a elipse, logo . Temos, então:
Integrando isso aqui, temos:
Logo, temos:
Passo 4
Agora precisamos parametrizar essa reta que criamos.
Temos uma reta que pertence ao eixo , portanto, podemos parametrizá-la assim:
Pela figura, como vamos fazer no sentido contrário ao dela para ter orientação positivos, vemos que vai de até .
Passo 5
Vamos agora derivar essa parametrização:
Passo 6
Agora vamos substituir esses valores na fórmula:
Aplicando a parametrização na expressão do campo:
A integral fica:
Como
Temos a integral que queremos
Lembrando que