Calcule , onde é o arco da circunferência , no primeiro quadrante, orientado no sentido anti-horário.
Passo 1
Vamos fazer um esboço da curva:
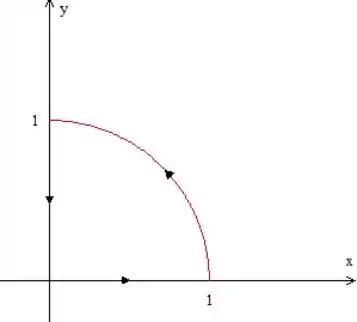
A parametrização desse arco envolveria senos e cossenos, que, quando substituídos na expressão do campo vetorial, tornariam a integral muito complicada. Vamos, então, aplicar o Teorema de Green aqui.
Passo 2
Perceba que a curva em que vamos integrar não é fechada, ela é composta apenas pelo arco de circunferência. O que faremos então? Vamos fechá-la, formando uma curva , onde é o segmento de reta horizontal e o vertical. Vamos orientar essa curva de positivamente.
Teremos, então:
Agora, vamos isolar o termo que queremos, :
Como os segmentos e são simples de parametrizar, vamos calculá-los pela definição mesmo.
Passo 3
O campo vetorial da questão pode ser escrito como
Vamos agora calcular :
Sendo a fronteira da nossa região , aplicando o teorema de Green, temos:
Calma, essa ainda não é a resposta, ainda precisamos calcular a integral em e em . Guarde esse resultado.
Passo 4
Vamos parametrizar os segmentos e .
Para : Este é um segmento horizontal em que e varia, portanto, podemos parametrizá-lo assim: , onde varia de a .
Para : Este é um segmento vertical em que e varia, portanto, podemos parametrizá-lo assim: , onde varia de a .
Passo 5
Agora precisamos derivar essas parametrizações:
Passo 6
Substituindo esses valores na fórmula que vimos capítulo passado:
Temos:
Passo 7
O que queremos é a integral em . Temos que:
Substituindo os resultados que encontramos: