Questão 2: Calcule a integral de linha
Onde é o trecho da curva , do ponto ao ponto .
Passo 1
Antes de começarmos o nosso problema em si, vamos fazer uma pequena mudança: particularmente acho além de feio, confuso, aquela notação de integral de linha ali no enunciado, então vamos mudar:
Essa então é a integral de linha que queremos resolver, onde o campo vetorial é...
Não se preocupe com o que acabamos de fazer, foi apenas escrever a integral de linha de uma forma mais elegante ! Porém, isso não é tão importante assim, pois o que queremos fazer mesmo é resolvê-la aplicando o Teorema de Green:
O motivo de utilizarmos esse teorema é simples de termos que utilizar o Teorema de Green ao invés de calcularmos direto... Aquela exponencial não é nada bonita. Mas se ainda você tiver dúvidas de que realmente o Green vai nos ajudar... Venha comigo!
Passo 2
Vamos calcular essa subtração e Green e verificar o que é mais fácil...
e são componentes, do campo...
Logo...
E
Então...
Veja que essa subtração é muito mais elegante de simples que o próprio campo, e isso nos sugere Green mesmo, saca?
Passo 3
Bem, mas para aplicar o Teorema de Green precisamos no mínimo nos certificar se o teorema de fato pode ser aplicado, neh? Esse teorema, como já deve saber, exige três condições:
- Curva fechada que delimita a região .
- Sem singularidades onde estamos trabalhando.
- Curvas orientadas positivamente.
Vamos verificar cada uma a partir de agora, ok?
Passo 4
A começar pela curva que deve ser uma curva fechada. A nossa curva é o gráfico de:
Ou seja... A parábola:
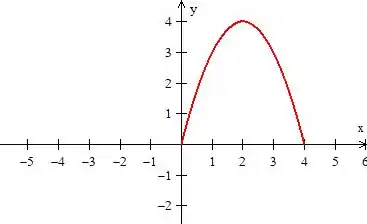
Veja que ela passa justamente por dois pontos interessantes: e . Eles são interessantes, pois o enunciado restringe a nossa curva apenas entre esses pontos que ela corta o eixo :
“... do ponto ao ponto .”
Pronto, mas já deu pra sacar que a curva é aberta, neh, e teoricamente não podemos aplicar o teorema de Green não. Mas não se preocupe que temos uma “carta na manga”: ora, se a curva é aberta, então a fechamos com outra curva:
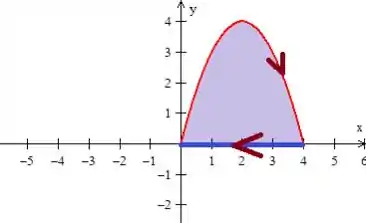
No caso pode ser essa reta passando por , mesmo. Só para não nos perdermos, vamos chamar essa reta de . AH! E com isso, temos uma região fechada por duas curvas:
Passo 5
A outra preocupação de Green se refere ao campo . De acordo com ele, temos que ter um campo sem singularidades onde estamos trabalhando, ou seja, sem problemas de definição:
E veja que o nosso não tem nenhum!
Passo 6
Por último, temos que ter uma curva girando no sentido anti-horário, para estar orientada no sentido positivo:
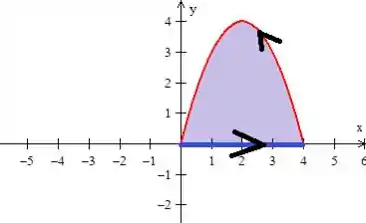
Porém, a nossa curva, originalmente está girando no sentido horário, então na igualdade de green, devemos multiplicar por a integral dupla, saca?
Assim, podemos colocar as curvas girando no sentido que a gente quer:
E agora estamos obedecendo também !
Passo 7
Com isso, sendo satisfeito, todas as condições do Teorema, podemos finalmente aplicar Green...
Como ...
O que queremos é a integral em (na curva cúbica), então devemos isola-la:
Bora calcular cada uma dessas duas integrais?
Passo 8
Começando pela integral dupla:
Veja que temos que descrever a região e para isso, vamos olhar pra ela mais uma vez:
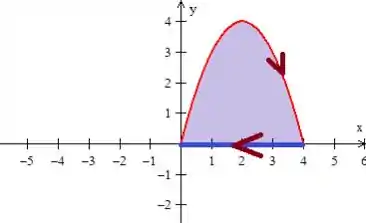
Podemos descrevê-la como região do tipo , onde o varia em um intervalo numérico bem definido:
Enquanto o varia de uma base e um teto (no caso a base é a reta e o teto é a parábola):
Assim:
Passo 9
Vamos agora para a última integral... A de linha:
- A primeira coisa é parametrizar a curva (que é uma reta e tem )...
- Agora temos que ter o ...
- Devemos também, trocar os termos do campo...
Onde o parâmetro dessa reta varia de até ...
Porém, esse aponta para a direita, sendo que nós sabemos que ele deve apontar pela esquerda...
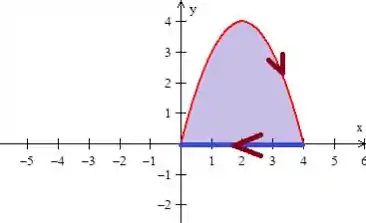
Agora é só substituir mesmo:
Passo 10
Beleza, voltando para a integral onde paramos, no passo :