Seja uma curva simples por partes, contida no conjunto aberto:
Com exceção no ponto inicial e do ponto final . Supondo que a área limitada pela curva e pelo eixo cartesiano é dada por , calcule:
Passo 1
Como não temos a equação que descreve a curva para utilizar a definição de integral de linha, a única saída aqui é aplicar o Teorema de Green. Mas primeiro temos que analisar a orientação da curva e ver se ela é fechada.
Vamos fazer um esboço dessa curva . Sabemos que ela vai do ponto ao ponto , sempre com e , ou seja, não é fechada. Como temos o valor da área entre essa curva que o eixo , vamos fechá-la com um segmento de reta desse eixo, criando um domínio cuja área conhecemos. Mas ainda temos um problema: podemos orientar positivamente o segmento de reta, mas a curva está orientada no outro sentido pelo próprio enunciado.
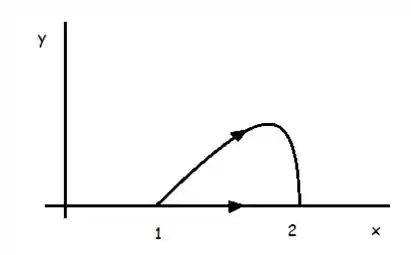
O que nós queremos é (a mesma curva, com orientação oposta). Teremos:
Mas nós já vimos que quando invertemos a orientação de uma curva temos:
Então podemos reescrever:
Passo 2
O campo vetorial pode ser escrito como
Vamos agora calcular :
Passo 3
Aplicando o teorema de Green, temos:
Conforme dito no enunciado, a área entre a curva e o eixo vale Assim, temos que
Agora precisamos calcular a integral ao longo de .
Passo 4
Temos um segmento de reta em que e varia entre e , portanto, podemos parametrizá-lo assim:
Derivando essa parametrização, temos:
Passo 5
Substituindo esses valores na fórmula que vimos capítulo passado:
Passo 6
O que queremos é a integral sobre ,então, vamos substituir esses valores em: