Questão 3:
Seja o campo vetorial plano
e seja o caminho orientado dado pela concatenação das curvas regulares orientadas , e , onde é o segmento que parte do ponto e vai até , é o arco da curva , partindo de até o segmento que parte de até .
Calcule .
Dica: Feche o caminho com um arco da curva indo de até para obter um caminho simples.
Passo 1
Uma integral de linha sempre nos dá vários caminhos para escolher:
1º - Resolução pelo Método Direto.
2º - Resolução pelo Teorema de Green.
Quero que você entenda aqui que não vamos resolver pelo método direto e quero que você entenda também o porquê: primeiro porque o campo é muito complicado
Segundo porque a curva , junção de outras três, mesmo sem esboçar já sabemos que não será algo elegante. E a terceira justificativa... É a famosa subtração de derivadas parciais:
Se ela for fácil, será a justificativa máxima para se aplicar Green. Então vamos calcula-lo?
Passo 2
Como o e são...
Calculando a primeira derivada parcial não se esquecendo da regra da cadeia...
Calculando a segunda derivada...
Calculando a subtração...
Como a subtração foi , muito simples, vamos de fato usar o teorema de Green :D!
Passo 3
O teorema de Green é...
Mas é claro, não podemos aplicar essa igualdade sem antes avaliar as condições do Teorema que nos exige:
1º - Uma região fechada pela borda .
2º - Orientada positivamente.
3º - Um campo sem singularidades.
Então vem comigo para averiguar isso aí mais de perto.
Passo 4
Bem, se desenharmos a curva conforme o enunciado, vamos perceber que ela é uma curva aberta. Veja só...
A curva que é um segmento paralelo ao que liga ... é um pouquinho mais chato, pois se trata de um pedaço da curva cúbica... , que une até o ... por fim é outro segmento que sai de e vai até .
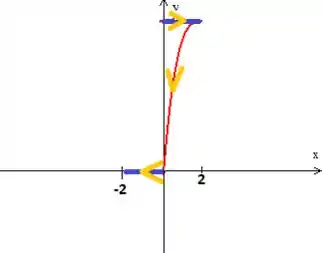
E pronto! Essa é a curva . Ela é obviamente aberta, por isso vamos seguir a dica do problema e fecha-la com uma translação da curva , a ...
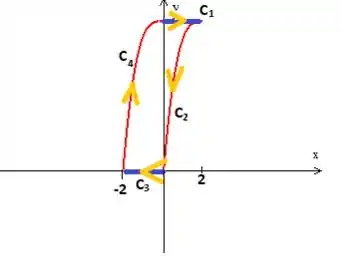
Sacou? Vamos chamar essa curva de . Mas lembre-se: Embora adicionamos a curva ao problema para aplicar o Teorema, ela não faz parte da curva que queremos a integral de linha, a curva ;)
Então, como a borda da região é e ...
Passo 5
Em relação ao orientada positivamente, a curva deveria estar girando no sentido anti-horário, mas você pode perceber que isso não acontece. Mas não se preocupe, porque corrigir isso é bem easy: basta multiplicar a integral dupla por ...
Passo 6
A última condição se trata do campo não ter singularidades, o que já acontece belezinha:
Afinal, ele não tem problema como uma divisão por ou coisa assim.
Passo 7
Assim, estando nas condições, podemos aplicar a igualdade do Teorema...
Como queremos calcular a integral de linha em cima de , podemos isola-la...
Passo 8
Vamos começar aqui então a calcular a integral tripla...
Bem, a integral dupla de é a área de região
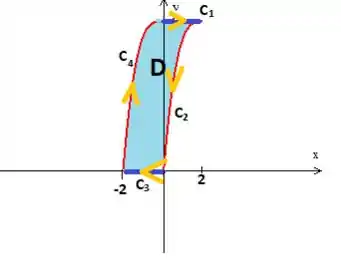
Porém, como pode comprovar, não fazemos a menor ideia de como calcular isso, por isso, vamos resolver a integral mesmo descrevendo a região como do tipo :
1º - varia entre funções.
2º - , entre números.
Mas repare que precisaremos separar em duas integrais iteradas, afinal em uma parte, o varia de até a curva e em outra parte, de até :
- Quando ...
- Quando ...
o ...
Como a curva tem o e a curva ... ...
Com o primeiro intervalo, construímos...
E com o segundo...
Assim...
Passo 9
Calculando isso aí, começando pela primeira integral...
Calculando a segunda integral dupla...
Passo 10
Então calculemos agora a integral de linha sobre a curva que adicionemos...
Primeiro precisamos de parametrizar . Como ele é uma cura com uma equação explícita...
Podemos parametrizar também de uma forma explicita:
Assim...
O parâmetro , por ser e varia de a ...
Encontrando o ...
Substituindo também os termos da parametrização no campo vetorial...
Substituindo tudo na integral...
Passo 11
Calculando...
Passo 12
Voltando então para a integral que queremos que vimos lá no inicio