Sejam os campos vetoriais definidos como:
Calcule
Sendo o arco da circunferência de raio , que liga a com
Passo 1
Vamos pensar o seguinte nessa questão, calcular essa integral de linha vai ser bem complicado principalmente por causa da complexidade do campo, né? Vamos tentar então usar o Teorema de Green. Para isso, precisamos calcular o rotacional de que é a soma de com .
Tem um detalhe aqui que vai nos ajudar a organizar a questão. Existe uma propriedade que diz que “o rotacional da soma dos campos é igual a soma dos rotacionais”, em outras palavras:
Precisamos então calcular esses dois rotacionais para depois usar o Teorema de Green, vamos lá?
Passo 2
Vamos então calcular o rotacional de , primeiro derivamos em função de , considerando constante:
Vamos ter que usar a regra do produto nessa derivada aqui, fica assim:
Agora derivando em relação a , considerando constante:
Também aplicando a regra do produto aqui:
Portanto, como as duas derivadas são iguais, nosso rotacional fica igual a zero!
Passo 3
Vamos fazer o cálculo do rotacional de agora! Derivando em relação a :
Derivando em relação a :
Logo o rotacional vai ser:
Passo 4
Aplicando agora a propriedade da soma dos rotacionais, temos que:
Pronto, agora é só aplicar o Teorema de Green! Para fazermos isso, vamos analisar nossa curva :
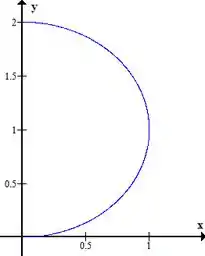
Vemos que ela não é fechada! Mas isso não é problema, já sabemos também que, em questões assim, podemos escolher uma curva simples para fechar a região e aplicar o Teorema de Green, é exatamente isso que faremos!
A curva mais simples para fechar essa região parece a reta que liga a , fica assim então:
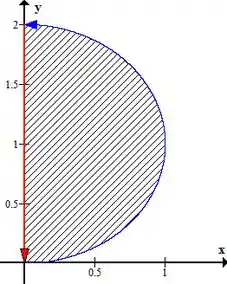
Beleza, agora precisamos aplicar o Teorema de Green! Se você não lembra, seu enunciado é esse aqui:
Passo 5
Calculamos que o rotacional de . Portanto nossa integral dupla fica:
Que nada mais é do que a área da nossa região! No caso, como temos uma semi-circunferência, nossa área fica:
Passo 6
Vamos para a outra integral que precisamos calcular, a da curva que criamos. Para calcular sua integral de linha vamos primeiro escolher uma parametrização fácil! Como nossa curva é uma reta em que , podemos parametrizar como:
Perceba que, para manter o sentido correto, precisamos fazer a nossa função de forma a ir de até , por isso colocamos essa parametrização um pouco diferente.
Analisando o nosso campo vetorial com a nossa nova parametrização:
Vamos então calcular a derivada na nossa curva :
Tendo isso, podemos agora calcular a integral de linha da nossa função:
Passo 7
Pronto! Calculamos a nossa integral dupla e a integral da curva que usamos para fechar a região, voltando para o nosso Teorema de Green:
Conclui-se, com os resultados que tivemos lá em cima: