Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas Abertas

Ver Teoria
Exercício 20123456789101112131415161718192122232425262728293031323334353637383940414243

Enunciado

Considere o campo vetorial F → no plano dado por

F → x ,   y = x 3 + x y 2 ,   3 x + x 2 y + y 3 .

Calcule a integral de linha ∫ C F → ∙ d r → , onde C é a parte da elipse x 2 9 + y 2 4 = 1 contida no primeiro quadrante, com ponto inicial ( 3 ,   0 ) e ponto final ( 0 ,   2 ) .

Passo 1

Vamos começar o nosso problema entendendo um pouco melhor quem é a curva C e como podemos chegar no resultado.

A curva C é formada por uma elipse com o eixo maior sobre x , pois se a gente lembrar da configuração geral dessa elipse: x 2 a 2 + y 2 b 2 = 1 com a > b ; e comparar com a que nós temos, vamos perceber que a = 3 que é maior que b = 2 . Logo

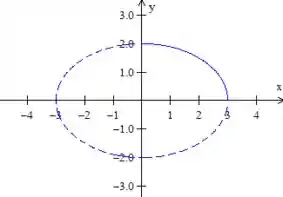
Note que não queremos a elipse toda e sim apenas esse pedaço no primeiro quadrante. :)

Passo 2

A gente poderia tentar resolver pelo método direto, porém note que daria um certo trabalho para substituir naquela função bizarra!

Ao invés disso, vamos tentar aplicar Green que nos fala que a integral de linha do bordo de uma superfície fechada é a integral do rotacional, dessa forma aqui:

∮ ∂ R F → ∙ d r → = ∬ R ∂ Q ∂ x - ∂ P ∂ y d x d y

Lembrou?!:D

Ok! E quem é mesmo esse bordo ∂ R ? É a borda dessa superfície fechada aqui

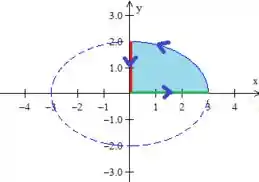
Logo, como a borda é formada pela união de três curvas, a C em azul, a C 1 em vermelho e C 2 em verde, teremos para aplicar o nosso amigo Green

∮ C F → ∙ d r → + ∮ C 1 F → ∙ d r → + ∮ C 2 F → ∙ d r → = ∬ R ∂ Q ∂ x - ∂ P ∂ y d x d y

Bem, agora é só calcular essas três integrais aí, que eu prometo ser mais simples que calcular esse integral direto. Bora lá?!

Passo 3

Vamos então começar com essa integral dupla aí. Lembrando que esse Q é a primeira entrada do vetor F → e P é a segunda, ou seja, F → = P x , y ,   Q x ,   y = x 3 + x y 2 ,   3 x + x 2 y + y 3 , teremos então

∂ Q ∂ x = 3 + 2 x y

∂ P ∂ y = 2 x y

Então, o rotacional que é ∂ Q ∂ x - ∂ P ∂ y nos dará

∬ R ∂ Q ∂ x - ∂ P ∂ y d A = ∬ R ( 3 + 2 x y - 2 x y ) d A     ⇒

∬ R 3 d A = 3 ∬ R d A

Essa resultado aí nos diz que essa integral dupla é três vezes o valor da área da região R . Pois então, a área dessa região R é 1 / 4 da área total dessa elipse

∬ R d A = 1 4 Á r e a e l i p s e

Se lembra daquele bizu da área da elipse (área = produto dos eixos por π , ou melhor, a ∙ b ∙ π )? Se a gente tem aqui que a = 3 e b = 2 , então

∬ R ∂ Q ∂ x - ∂ P ∂ y d A = 3 1 4 Á r e a e l i p s e = 3 4 3 ∙ 2 ∙ π

Ou seja,

∬ R ∂ Q ∂ x - ∂ P ∂ y d A = 9 π 2

Passo 4

Falta agora resolver aquelas duas integrais de linha. Mas relaxa que elas são mais simples pois as “linhas”, ou melhor, as curvas C 1 e C 2 são mais fáceis de parametrizar, veja só

  • C 1 é uma reta que tem x = 0 e y está indo de 2 até 0 , logo, podemos parametrizar

    • γ 1 t = ( 0,2 - t )

    Onde y = 2 - t e 0 ≤ t ≤ 2

  • Enquanto que C 2 é uma reta que tem y = 0 e x está indo de 0 até 3 , logo, podemos parametrizar

γ 2 t = ( t , 0 )

Onde x = t , e 0 ≤ t ≤ 3

Pois bem, vamos resolver essas integrais de linha separadamente, okay?

Passo 5

Começando pela ∮ C 1 F → ∙ d r → , devemos obter o termo d r → = γ 1 ' t d t

Derivando a curva γ 1 t = ( 0 ,   2 - t ) em relação a t

γ 1 ' t = ( 0 ,   - 1 )

Logo

d r → = γ 1 ' t d t = 0 ,   - 1 d t

Agora aplicando na integral de linha

∮ C 1 F → ∙ d r → = ∫ 0 2 x 3 + x y 2 ,   3 x + x 2 y + y 3 ∙ 0 ,   - 1 d t

E resolvendo esse produto escalar:

∮ C 1 F → ∙ d r → = ∫ 0 2 - y 3 - x 2 y - 3 x d t

Epa!!! Estamos integrando em t , logo devemos substituir a nossa parametrização nessa função, ou seja, como γ 1 t = ( 0 ,   2 - t ) , x = 0 e y = 2 - t

∮ C 1 F → ∙ d r → = ∫ 0 2 - 2 - t 3 d t

Fazendo uma substituição simples do tipo 2 - t = u , d u = - d t , enquanto que os limites, quando t = 0 → u = 2 e t = 2 → u = 0

∮ C 1 F → ∙ d r → = ∫ 2 0 u 3 d u

∮ C 1 F → ∙ d r → = u 4 4 2 0

Substituindo os limites

∮ C 1 F → ∙ d r → = - 2 4 4 = - 4

Passo 6

Repetindo o processo para ∮ C 2 F → ∙ d r →

d r → = γ 2 ' t = ( 1 ,   0 )

∮ C 2 F → ∙ d r → = ∫ 0 3 ( x 3 + x y 2 ,   3 x + x 2 y + y 3 ) ∙ 1 ,   0 d t

∮ C 2 F → ∙ d r → = ∫ 0 3 x 3 + x y 2 d t

Substituindo a parametrização de γ 2 t = ( t , 0 ) da curva C 2

∮ C 2 F → ∙ d r → = ∫ 0 3 t 3 d t = t 4 4 0 3

∮ C 2 F → ∙ d r → = 81 4

Passo 7

Voltando para Green...

∮ C F → ∙ d r → + ∮ C 1 F → ∙ d r → + ∮ C 2 F → ∙ d r → = ∬ R ∂ Q ∂ x - ∂ P ∂ y d x d y

∮ C F → ∙ d r → - 4 + 81 4 = 9 π 2

Isolando ∮ C F → ∙ d r → , obteremos

∮ C F → ∙ d r → = 9 π 2 - 81 4 + 4

Resposta

∮ C F → ∙ d r → = 18 π - 65 4

Exercícios de Livros Relacionados

Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = x + y 3 , x 2 + y C consiste no arco da curva y = sen ⁡ x de ( 0,0 ) a ( 0 ,
f ( x , y ) = (x + y^2) // sqrt(1 + x^2) , C : y = x^2 // 2 entre ( 1,1 // 2 ) e ( 0,0 )
f ( x , y ) = x^3 // y , C : y = x^2 // 2 , 0 = x = 2