Calcule para a curva dada por com percorrida no sentido anti-horário.
Passo 1
Para escrever a curva na forma paramétrica teríamos que usar senos e cossenos, o que tornaria a integral muito complicada. Portanto, calcular essa integral pela definição não é uma boa. Vamos tentar usar o Teorema de Green aqui então.
O campo vetorial da questão pode ser escrito como
Vamos agora calcular :
Essa é uma expressão simples, quer dizer que estamos no caminho certo!
Passo 2
Beleza, vamos aplicar Green então, mas em que região? Vamos primeiro descobrir quem é essa curva do enunciado:
Completando esses quadrados, temos:
A equação é uma circunferência de raio centrada em , certo?
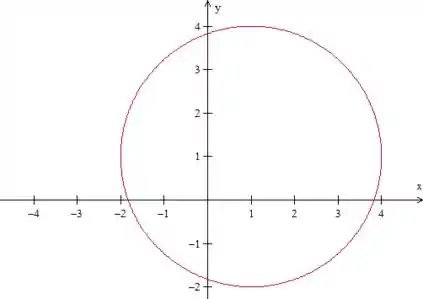
Como o problema diz que , temos isso aqui:
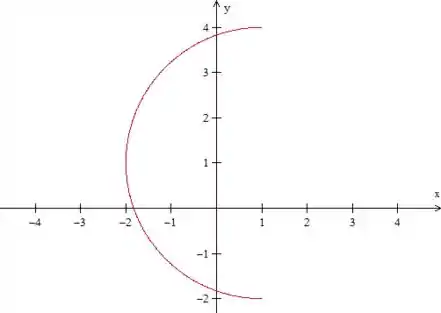
Mas para aplicar o Teorema de Geen, nós precisamos de uma curva fechada e orientada positivamente, não é? Vamos fechar isso aí com uma reta:
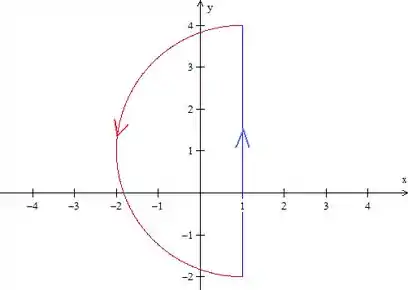
Como o enunciado já dizia que está orientada no sentido anti-horário, tá tudo ok então.
Agora podemos aplicar Green:
Onde é a reta do desenho e é a região entre o arco e a reta.
Passo 3
Como a região está compreendida entre um arco de circunferência e uma reta, a melhor saída aqui são as coordenadas polares. Faremos:
Esses termos que adicionamos na mudança polar estão aí porque a circunferência está deslocada da origem, lembra? Temos . Adicionando os termos , nós “levamos” o novo sistema de coordenadas para o centro da circunferência, que passa a ser escrita como .
Isso ocorre porque o da mudança polar faz desaparecer o da equação da circunferência, tornando sua equação .
Bom, sabemos então que . Como temos meia volta da circunferência, olhando para o gráfico e lembrando que o novo eixo de coordenadas está no seu centro, vemos que .
Agora, fazendo a mudança polar na integral, temos:
Passo 4
Agora precisamos parametrizar essa reta que criamos.
Temos um segmento que pertence à reta (para qualquer ), portanto, podemos parametrizá-lo assim:
Pela figura, vemos que .
Agora vamos substituir esses valores na fórmula:
Aplicando a parametrização na expressão do campo:
A integral fica:
Passo 5
Agora vamos encontrar o que queremos: