Considere a curva parametrizada por ,com
A integral é igual a:
Passo 1
Logo de cara você já deve ter percebido que resolver isso aí pelo método direto pode não ser mto legal. Essa parametrização dentro desse campo não ia dar nada mto bonito. Com isso a gente automaticamente pensa no teorema de green. Uma das condições do teorema é termos a curva fechada, certo? Vamos ver se essa curva aí é fechada simplesmente observando os extremos da parametrização.
varia entre 0 e 1.
Opa, como começa e termina em diferentes pontos, isso nos mostra que estamos trabalhando com uma curva aberta. Pra isso, vamos simplesmente fechá-la com a curva mais simples possível, que nesse caso é uma reta ligando os dois pontos.
Então com isso agora o teorema fica:
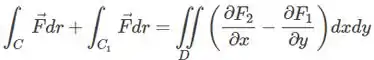
Onde será essa reta ligando os pontos, e .
Passo 2
Vamos agora então calcular o rotacional que vai na integral dupla.
Opa, isso já dá uma facilitada legal na nossa vida, uma vez que a integral dupla já zera toda!
Partindo agora pra integral de linha em cima da reta.
Passo 3
Começamos parametrizando a curva que liga os pontos (0,1) ao (0,-1)
Depois disso tiramos a derivada da parametrização.
E comtamos nossa integral, sem esquecer de escrever o campo em função da parametrização.
Passo 4
Agora é só resolver essa integral: