Seja uma curva orientada, composta dos segmentos de reta que ligam os pontos a , a , a , onde e são números reais positivos. Mostre que:
Para qualquer função de classe definida em todo .
Passo 1
Essa questão tá bem estranha, né?
Não dá pra calcularmos direto porque não sabemos que função é essa, mas vamos tentar imaginar essa curva aí pra ver se temos alguma dica, se alguma coisa vai cancelar ou sei lá.
Ele só diz que e são positivos, então não dá pra saber exatamente onde que é cada ponto, mas, de forma geral, temos alguma coisa assim:
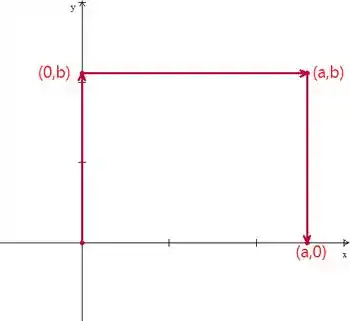
Que é mais ou menos um retângulo, só falta a base. Mas isso já é uma ótima dica, porque a área desse retângulo é exatamente , então provavelmente o que queremos provar é que:
E a gente sabe que a área também pode ser calculada por uma integral dupla, então:
E o que a gente tem que relaciona uma integral dupla com uma integral de linha? O Teorema de Green!
Vamos tentar seguir esse caminho e ver se conseguimos resolver essa questão estranha...
Passo 2
Vamos lembrar do Teorema de Green:
Mas é importante saber que ele só vale pra curvas fechadas, não vai esquecer!
E como nossa , curva não é fechada, então na verdade vamos ter que criar uma curva auxiliar , que de preferência vai ser o segmento pra fecharmos nosso retângulo. Só temos que tomar cuidado com a orientação, então vamos ter então:
E, assim, vamos ter :
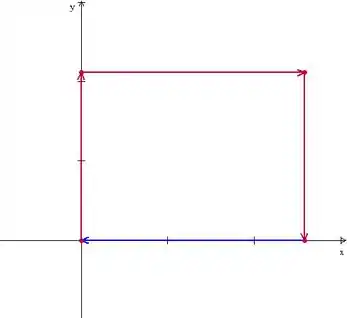
Só que assim tá orientada no sentido horário, e o teorema de Green manda a gente usar os sentido anti-horário, então vamos ter e a integral fica:
Então, se conseguirmos provar que:
A gente consegue resolver a questão. Mas vamos ver como calcular cada uma dessas integrais.
Passo 3
Vamos começar com aquela integral dupla e pra isso vamos ver essas derivadas aí:
Então:
Opa, estamos quase lá, só vamos ver como que fica aquela integral de linha ali.
Passo 4
A gente tem uma integral de linha vetorial, então vamos usar a fórmula:
A gente já tem a parametrização, então vamos encontrar o vetor tangente:
Então vamos ficar com:
Acho que foi, né? Vamos voltar aquela nossa relação pra conferir.
Passo 5
A gente tinha:
E conseguimos provar o que queríamos!
Mas que a questão era estranha, era...
Resposta
Ei, a resposta está no passo a passo :)