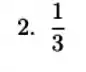![]()
Passo 1
A questão nos pede esse . Ou seja, ele nos pede o valor da derivada da inversa de quando vale (assim como a é função de , a sua inversa é função de ).
Pelo teorema da inversa, temos:
Nesse caso, temos que , ou seja, quando teremos .
Dessa maneira, valerá:
E temos do enunciado que . Enfim, o resultado é:
Resposta