Seja para
Determine uma expressão para a inversa de h neste intervalo
Esboce o gráfico de e da sua inversa no mesmo plano cartesiano
Passo 1
Bom, ele pede uma expressão para a inversa do cosseno. Adivinha qual será? A sua função inversa trigonométrica!
O cosseno vai de até , onde temos
Logo, o domínio de será de até .
Passo 2
Para esboçar o gráfico de e sua inversa, a dica é a seguinte:
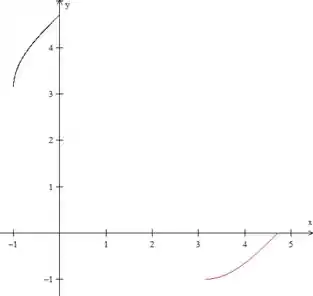
Começamos com o gráfico do cosseno, no seu domínio .
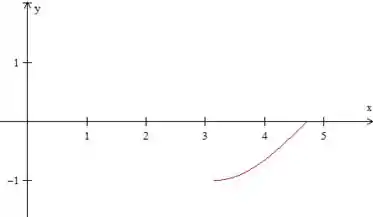
Para desenhar a inversa de qualquer gráfico, podemos desenhar um gráfico simétrico em relação à reta . Vamos traça-la e, então, desenhar um gráfico espelhado em relação a ela:
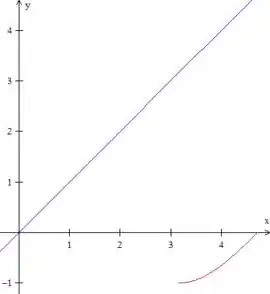
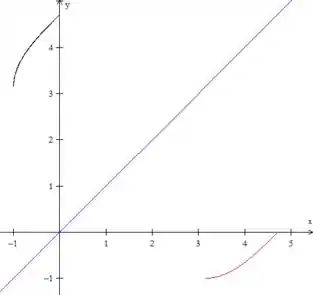
Agora basta tirar a reta daí: