Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivada da Função Inversa

Ver Teoria
Exercício 71234568910111213141516171819202122232425262728293031323334353637383940414243

Enunciado

Seja

g x = 5 + log 1 5 ⁡ ( 2 + x )

a) Calcule g ( 3 )

b) Determine g ' , a derivada da função g

c) A função g é inversível? Justifique.

d) Determine a expressão para g - 1 , a inversa da função g

e) Esboce o gráfico de g , assinalando os pontos onde o gráfico intercepta os eixos.

Passo 1

a) Para calcular g ( 3 ) basta substituir x = 3 na função.

g 3 = 5 + log 1 5 ⁡ ( 2 + 3 )

g 3 = 5 + log 1 5 ⁡ 5

g 3 = 5 - 1

g 3 = 4

Passo 2

b)

f ' x = 5 ' + log 1 5 ⁡ 2 + x '

f ' x = - 1 x log ⁡ 5 + log ⁡ 25

Passo 3

c) Sim, a função g é inversível. Sabe por quê? Porque ela é bijetora, ou seja, todos os valores de seu domínio (que é x > - 2 ) possuem um único valor de y associado e todos os y da imagem estão associados com um x do domínio.

Passo 4

d) Para encontrar a inversa de g devemos isolar o x e encontrar um nova função cuja variável é y .

y = 5 + log 1 5 ⁡ ( 2 + x )

y = 5 - log 5 ⁡ ( 2 + x )

log 5 ⁡ ( 2 + x ) = 5 - y

5 5 - y = 2 + x

x = 5 5 - y - 2

Portanto,

g - 1 y = 5 5 - y - 2

Passo 5

e) g intercepta o eixo x quando:

y = 5 + log 1 5 ⁡ ( 2 )

E g intercepta o eixo y quando:

5 + log 1 5 ⁡ 2 + x = 0

5 - log 5 ⁡ 2 + x = 0

log 5 ⁡ 2 + x = 5

5 5 = 2 + x

25 = 2 + x

x = 23

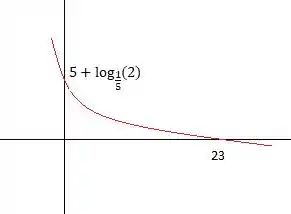
Agora é só esboçar o gráfico, que fica desse jeito:

Resposta

  1. g 3 = 4
  2. f ' x = - 1 x log ⁡ 5 + log ⁡ 25
  3. Sim
  4. g - 1 y = 5 5 - y - 2

Exercícios de Livros Relacionados

f (x) = int_x^2 t d t , x0 ; d = - 6
Calculec) cos (a r c s e n (- (sqrt(3))/(2)))
Calcule.j) a r c s e n (- (sqrt(3))/(2))
Calculed) s ec (a r c t g 1)
Calcule.d) a r c t g 1