Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Derivada da Função Inversa

Ver Teoria
Exercício 34123456789101112131415161718192021222324252627282930313233353637383940414243

Enunciado

Seja

f x = 1 - x 3 ,   x ≤ 0 1 - x 2 ,   x > 0

Se f - 1 existir, calcule ( f - 1 ) ' ( x ) e esboce os gráficos de f e f - 1 .

Passo 1

Como a função é dividida em parte e as duas partes são funções polinomiais, a função é contínua para todo x ϵ R . Como consequência, podemos concluir que f é diferenciável para todo x ϵ R . A primeira condição do Teorema da Função Inversa foi atendida.

Vamos verificar a segunda, que diz que f ' ( x ) ≠ 0 .

f ' x = - 3 x ² ,   x ≤ 0 - 2 x ,   x > 0

Sendo assim, o Teorema da Função Inversa é valido e a função possui inversa.

Passo 2

Para determinar a inversa, vamos isolar x , colocando-o em função de y

f - 1 ( y ) = 1 - y 3 ,   y ≥ 1 1 - y   ,   y < 1

Passo 3

Agora podemos derivar f - 1 ( y ) .

( f - 1 ) ' ( y ) = - 1 3 ( 1 - y ) ² 3 ,   y > 1 - 1 2 1 - y   ,   y < 1

Mudando para a variável x :

( f - 1 ) ' ( x ) = - 1 3 ( 1 - x ) ² 3 ,   x ≤ 0 - 1 2 1 - x   ,   x > 0

Passo 4

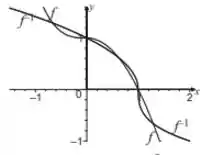
Pra finalizar, os esboços dos gráficos de f e f - 1 são;

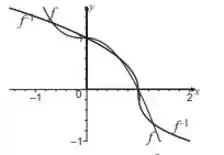
Resposta

( f - 1 ) ' ( x ) = - 1 3 ( 1 - x ) ² 3 ,   x ≤ 0 - 1 2 1 - x   ,   x > 0

Exercícios de Livros Relacionados

f (x) = int_x^2 t d t , x0 ; d = - 6
Calculec) cos (a r c s e n (- (sqrt(3))/(2)))
Calcule.j) a r c s e n (- (sqrt(3))/(2))
Calculed) s ec (a r c t g 1)
Calcule.d) a r c t g 1