Questão 2:
Seja .
- Considere como domínio de o maior possível para que seja inversível e para que o gráfico de (a função inversa de ) passe pelo ponto . Nestas condições, determine o domínio de , o domínio de , e uma expressão para .
- Determine a equação da reta tangente ao gráfico de em .
Passo 1
Bem, normalmente quando vamos falar de função inversa se conseguirmos desenhar um esboço do gráfico da função, nos ajuda muito. No nosso caso, é uma função parecida com o cosseno, então conseguimos sim desenha-la:
Perceba que quando ... O cosseno assume o mesmo valor de ...
Então
Agora quando
Colocando esses pontos no gráfico e lembrando que o gráfico do cosseno é semelhante a senoide, ganhamos o esboço da nossa ...
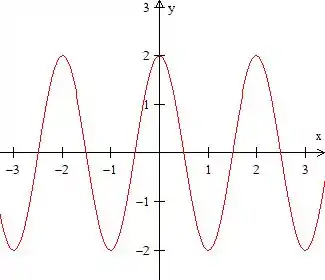
Passo 2
Queremos encontrar o maior domínio que existe uma função inversa e, além disso, ela deve passar pelo ponto .
Repare que, infelizmente, esse domínio que está esboçado aí não serve para o domínio da inversa, pois ele é grande demais. Você quer ver uma prova?
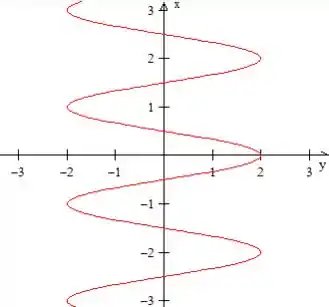
Como a função inversa é como se girássemos à direita o gráfico... Quando fazemos isso...
Isso é uma função? Não! Pois se traçarmos uma reta vertical ela vai cortar o gráfico duas vezes ou mais.
Seria função então se o domínio fosse, por exemplo, de a (em )... Ou outro domínio possível seria de a , e assim por diante sacou?
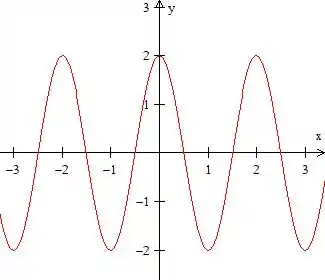
Beleza, já sabemos o tamanho do maior intervalo e já até vimos alguns intervalos que funciona, mas agora qual deles vamos pegar?
Essa pergunta se responde observando que o problema não quer qualquer intervalo, e sim aquele que contém o ponto . Como esse ponto pertence ao intervalo já da função inversa, esse se refere ao e esse , saca?
Então basicamente já matamos a charada, queremos o intervalo que contém o ponto onde , ou seja, o intervalo de a , e ele é o maior possível já, sacou?
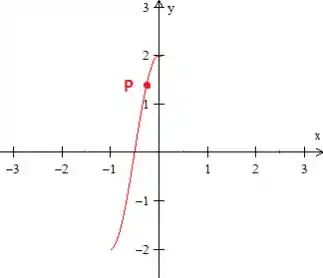
Passo 3
Agora queremos obter o domínio da função inversa . Bem, com o método gráfico isso é bem easy. Veja novamente o gráfico da nossa função com o maior intervalo onde ela contém iversa que queremos...
Se girarmos novamente o gráfico, vamos obter o desenho da inversa...
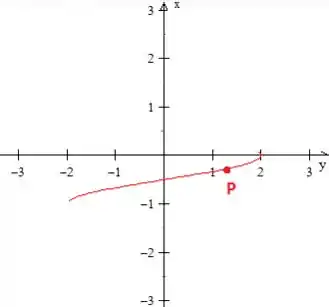
Qual é o domínio que você pode notar? Lembre-se que na inversa, o domínio está em (o que está deitado)
Isso mesmo, de a .
De uma forma mais formal, podemos dizer que a imagem de é o domínio de ...
Passo 4
Por fim, para obter a expressão da inversa, isolemos o ...
Chamando ...
Cuidado! Pois normalmente tenderíamos a simplesmente colocar...
Que é a inversa do cosseno. Mas isso tem um problema aqui. Veja só, já sabemos que varia de a . Se colocarmos ali no lugar dele...
Agora qual é o arco cujo cosseno é ? A resposta é , pois arco-cosseno é uma função considerada positiva. Embora sabemos que , também é resposta para o problema. Então...
Mas no gráfico da inversa o que corresponde o é , logo, devemos multiplicar esse aqui por ...
Se chamarmos , eis a função inversa...
Repare que essa já é a resposta, mas é feio deixar assim. É mais bonitinho ter o como uma variável, pelo menos os matemáticos acham isso. Por isso vamos aqui mudar essa letra de para , mas isso é só um nome, heim...
Passo 5
Bem, a equação da reta tangente a um ponto da inversa de é dado por...
Para o ponto ...
Repare que precisamos da derivada da função inversa no ponto . De acordo com o teorema da função inversa, podemos derivar essa função aí em qualquer ponto pela fórmula...
Com ...
Qual o arco cujo cosseno é ? ...
Então...
Qual é a derivada da função ?...
Logo...
Logo...
Resposta
Maior domínio de nas condições dadas: