Considere a função tangente:
Determine o maior intervalo contendo tal que a função tangente restrita a este intervalo seja inversível;
Seja a inversa da função mencionada no item , determine uma expressão para em função de ;
Calcule .
Passo 1
Vou começar aqui reproduzindo o gráfico da tangente para caso você não lembre/conheça:
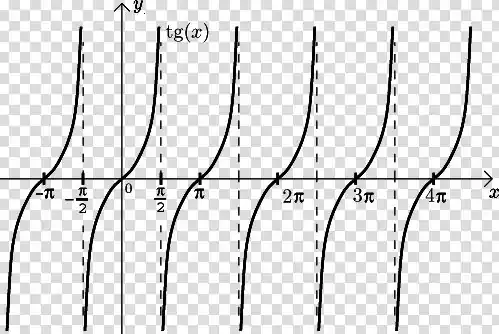
Como você deve reparar, o gráfico fica limitado entre , , , etc. Quer dizer, a função mantém um período de repetição. Em algum desses períodos nós temos o termo limitado. Ora, a pergunta da questão era sobre um intervalo tal que a função tangente seja inversível! Para ser inversível a função deve ser contínua. Então devemos determinar o período entre o qual está e esse será o nosso intervalo. No caso, temos que
Logo, o nosso intervalo seria nesse caso o .
Passo 2
Repara, ele tá mencionando uma função que trabalhamos no item . Não é muito claro, mas ele quer que invertamos justamente a parte do gráfico que está no intervalo .
Repara o seguinte, se fossemos inverter a parte da tangente do intervalo nós deveríamos escrever simplesmente que . Porém, estamos deslocados para frente, nesse intervalo (basta fazer ). Enfim, a função que a questão pede será:
Passo 3
Agora o cara espera que calculemos . Vamos derivar :
Substituindo :