- Apresente num gráfico a extensão ímpar e periódica de período da função
- Encontre a série de Fourier.
- Usando o método de separação de variáveis, encontrar a solução da seguinte equação de calor. Explique detalhadamente como se resolve o problema.
Onde é a função descrita no item (a).
Passo 1
(a )
Para esboçar esse gráfico, primeiro vamos colocar no plano o desenho dessa função :
Essa função é até e depois é , veja:
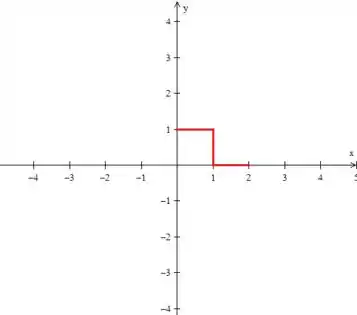
A extensão ímpar dela é a simetria com o eixo e invertendo o sinal, já que é ímpar. Em desenho:
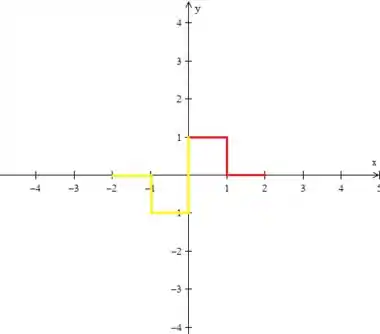
Veja que de fato, a extensão ímpar da função , e que vamos chamar de , é ímpar e tem um “tamanho” quatro, pois:
Agora é só colocar o padrão repetindo para a extensão se tornar periódica:
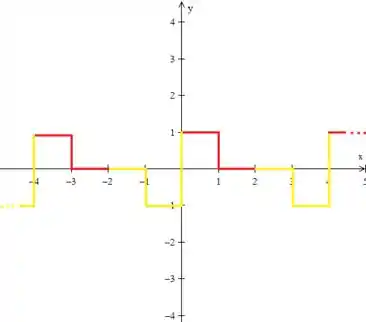
Ou seja, em matemática isso significa que a extenção ímpar e periódica de período de é:
Passo 2
(b)
Vamos lembrar nossas fórmulas, fera!
No nosso caso, !
Passo 3
Como e ímpar, são nulos.
Agora, vamos aplicar as condições do problema naquelas fórmulas para calcular os coeficientes.
Para par:
Para par:
Aplicando á formula da série de Fourier...
Passo 4
(c )
Vamos começar pela separação de variáveis e buscar por soluções do tipo:
Substituindo na equação
Passando tudo que tem para um lado e tudo que tem para o outro lado
Como essa igualdade vale para todo e todo , vamos igualá-la a uma constante
Separando a igualdade em duas equações, você vai encontrar isso aqui...
Substituindo as condições de contorno...
Passo 5
Isso nos dá um PVC em .
Esqueça, por enquanto, a condição que tem uma função:
Precisamos agora achar
Passo 6
Como temos um problema de autovalor, vamos montar e resolver a equação característica da equação de
Agora vamos analisar cada caso.
Se teremos duas raízes
Nas condições de contorno...
Neste caso, só teremos soluções triviais.
Se teremos duas raízes iguais a a solução da seguinte forma:
Que no nosso caso vai ficar...
Aplicando as condições iniciais
Também só há soluções triviais aqui !
Se , e a solução tem essa cara aqui
Como queremos soluções não triviais
Passo 7
Agora vamos trabalhar nossa função usando a condição inicial
Resolvendo a EDO de primeira ordem vamos ter
Agora sim,
Passo 8
Pelo princípio da superposição, podemos escrever a série
Vamos aplicar a condição:
Na verdade, a solução para essa condição é a série de Fourier da própria . A resposta será...
Resposta
(a )
(b)
(c )