Usando separação de variáveis, encontrar a solução da seguinte equação do calor. Explique detalhadamente como se resolve o problema
onde é definida como a extensão par e periódica de período da função onde e esboce o gráfico no intervalo .
Passo 1
Para resolver o problema por separação de variáveis, vamos escrever
Note que se trata de uma equação de calor.
Com a separação, teremos:
Portanto, nossa equação se torna
E isso origina duas EDO’s (uma em e outra em ):
Passo 2
Agora, vamos olhar para as condições de contorno:
De e , se , então ambas as condições seriam atendidas. Mas como isso implicaria em o que daria a solução trivial.
Passo 3
Neste caso, nos resta admitir o seguinte:
Assim, formamos o seguinte problema:
Buscando uma solução não-trivial , vamos avaliar a equação característica:
Temos um problema de contorno e vamos ter que analisar cada caso de .
Passo 4
Caso 1: . Ou seja, o que está dentro da raiz é positivo. Nesse caso, . As soluções são do tipo:
Calculando .
Agora vamos usar as condições de contorno:
Isso nos dá
Substituindo esses valores na nossa solução geral, temos
Mas isso não nos ajuda em nada! Essa é a solução trivial, que não nos interessa. Portanto, esse caso, , não nos dá soluções para a EDO.
Passo 5
Caso 2: . Nesse caso, . As soluções são do tipo:
Calculando
Agora vamos usar as condições de contorno:
Isso nos deixa com a solução
Vamos calcular para esse
Nossa solução fica
Temos que analisar agora a condição e isso vai nos dar que.
Passo 6
Caso 3: . Ou seja, o que está dentro da raiz é negativo. Nesse caso, . As soluções são do tipo:
Substituindo
Calculando
Aplicando as condições de contorno
Note que na última equação não podemos ter (se não teríamos ). Então, precisamos de . Como , sobra
Passo 7
Como queremos , basta fazer , de modo que obtemos . Estes são nossos autovalores!
Portanto, ficamos com
que são nada mais nada menos que nossas autofunções!
Passo 8
Agora que já conhecemos os autovalores , vamos voltar pra equação em :
Fácil, né? Vamos substituir por :
E, assim, uma solução deve ser
Passo 9
Agora vem o pulo do gato. Se qualquer é solução para , então uma combinação linear dessas soluções (para diferentes valores de ) também é solução:
Assim:
Sabendo que
Para calcularmos os coeficientes da nossa função temos que tratar a expansão em série de Fourier da nossa função .
Passo 10
Vamos primeiro achar essa nossa função. Se a função é par, então . Bom, assumimos então que . E como o período é , vemos que . Um esboço é ilustrado abaixo.
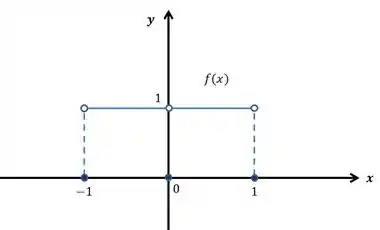
Passo 11
Agora que nós já sabemos como é a nossa função podemos escrever ela como uma série de Fourier e achar os coeficientes que estamos procurando.
Onde é o período; portanto, .
Passo 12
Vamos avaliar os coeficientes da série:
Note que as descontinuidades de não afetam a integral.
Agora, temos:
Além disso:
Passo 13
Combinando os resultados, a série de Fourier é simplesmente
Passo 14
No nosso problema de equação de calor os coeficientes são justamente os coeficientes da série de Fourier de : .
Lembre que e , então e . Logo, sobra um termo apenas:
Na realidade, a solução é exatamente .
Resposta