UFMG, Sem campus, Equações Diferenciais B, P1- 2022.2, Questão 2a
Considere o problema de condução de calor:
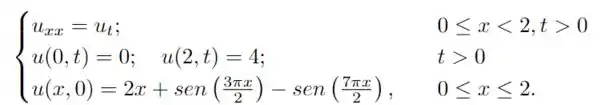
Encontre a solução estacionária do problema.
Passo 1
Oiiie, tudo bem com você?
Nós temos a construção usual de um problema de condução de calor em uma barra
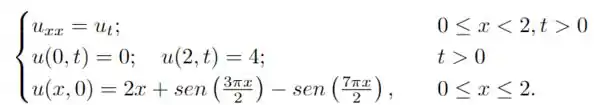
em que representa a temperatura ao longo do tempo e ao longo do comprimento da barra . Essa barra tem extremidades em e , e suas extremidades estão sendo mantidas à temperaturas e , além disso, sua distribuição de temperatura inicial ao longo da barra é .
Para encontrarmos a solução estacionária, vamos procurar uma solução da equação acima que não dependa do tempo, ou seja, estaremos procurando algo como
Isso será a nossa solução estacionária! Ótimo! Vem comigo!
Passo 2
Substituindo em nossa equação diferencial, obtemos que
em que usando as condições de contorno da barra, nos indica que e , já que em nosso problema, em todo instante de tempo essas são as temperaturas nas extremidades. Resolver esta equação diferencial é bastante direto, precisamos apenas integrar duas vezes, com a primeira integral obtemos a seguinte constante
e, com a segunda integral, temos que
Vamos agora aplicar as condições iniciais para encontrar essas constantes!
Passo 3
Usando que , temos que
portanto, temos que . Agora, usando que , com , temos
de forma que . A solução estacionária é dada então por
Belezinha! Essa foi a primeira alternativa! Guarde esse resultado que você irá precisar para resolver a alternativa . Te vejo na próxima! Até já!